\(\def \u#1{\,\mathrm{#1}}\) \(\def \abs#1{\left|#1\right|}\) \(\def \ast{*}\) \(\def \deg{^{\circ}}\) \(\def \tau{\uptau}\) \(\def \ten#1{\times 10^{#1}}\) \(\def \redcancel#1{{\color{red}\cancel{#1}}}\) \(\def \BLUE#1{{\color{blue} #1}}\) \(\def \RED#1{{\color{red} #1}}\) \(\def \PURPLE#1{{\color{purple} #1}}\) \(\def \th#1,#2{#1,\!#2}\) \(\def \lshift#1#2{\underset{\Leftarrow\atop{#2}}#1}}\) \(\def \rshift#1#2{\underset{\Rightarrow\atop{#2}}#1}}\) \(\def \dotspot{{\color{lightgray}{\circ}}}\) \(\def \ccw{\circlearrowleft}\) \(\def \cw{\circlearrowright}\)
Chapter 3: Linear Motion
14.

Slopes

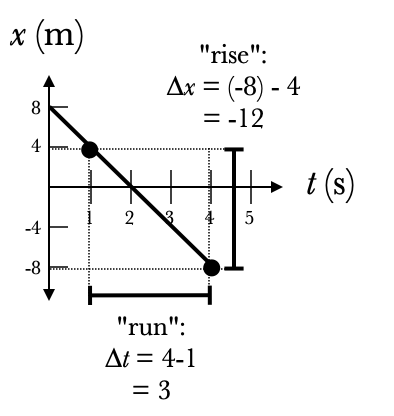
(no alternate text)

The slope of a graph is equal to the change in the vertical between two points divided by the change in the horizontal; colloquially this is described as "rise over run".

In the graph on the right, the "rise" is the change in the $x$ value: $\Delta x=-12\u{m}$. The "run" is the change in the $t$ value: $\Delta t = 3\u{s}$. Thus the slope of this line is $$\text{slope}={\Delta x\over\Delta t}=-4\u{m\over s}$$

This quantity, displacement divided by a time interval, is the average velocity between the two points:

The slope of a position graph gives you the velocity.

In this case, the slope is negative and so this object is moving to the left. Here is a more complicated position graph: