It can also be helpful to graph the velocity of an object over time, in addition to the position. The two graphs are not independent: the velocity at any time is the slope of the position graph. A turning point on a position graph corresponds to the place on the velocity axis where the curve crosses the horizontal axis.
Because acceleration is defined as
the slope of the velocity graph is the acceleration.
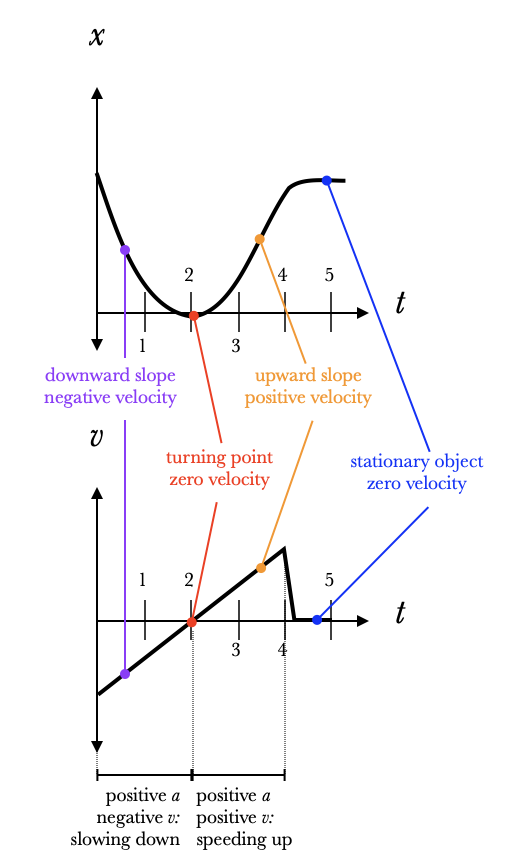
Consider this example to the right. The object has a positive acceleration until , and then a much larger negative acceleration before it comes to a stop. Remember that positive acceleration is not the same as speeding up: sign is about direction. In the first two seconds, this object has a positive acceleration but a negative velocity: the signs are opposite, which means that the object is slowing down (moving closer to zero). From until , the acceleration is still positive but now the velocity is also positive, so the object is speeding up (moving away from zero).
