13.
Graphing Position
Another way we can visualize motion, particularly in one dimension, is by graphing the position, velocity, or acceleration as a function of time. Time is always on the horizontal axis in such graphs.To make a position graph we need to define an origin (the point which we are calling "0") and a direction we're calling "positive" (often to the right, by convention.) The axis is usually labelled $x$ if the motion is horizontal and $y$ if it is vertical, although that's also a matter of convention: for an object moving along a diagonal, for instance, we could use either label.
Column

Column
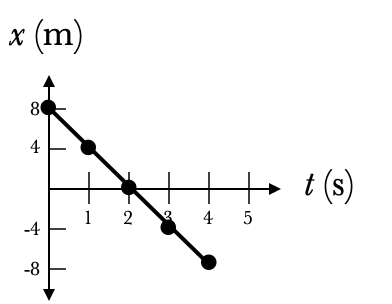
Column
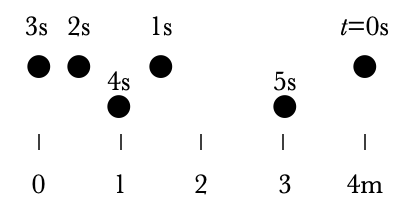
Column
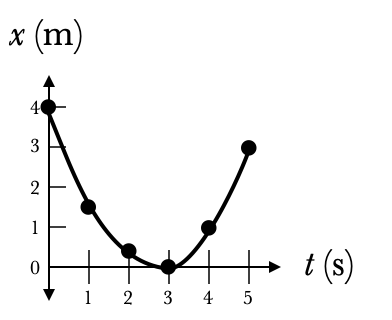
This is the corresponding graph. The minimum or maximum of a position graph is called a turning point, and occurs when the object changes direction.