\(\def \u#1{\,\mathrm{#1}}\) \(\def \abs#1{\left|#1\right|}\) \(\def \ast{*}\) \(\def \deg{^{\circ}}\) \(\def \tau{\uptau}\) \(\def \ten#1{\times 10^{#1}}\) \(\def \redcancel#1{{\color{red}\cancel{#1}}}\) \(\def \BLUE#1{{\color{blue} #1}}\) \(\def \RED#1{{\color{red} #1}}\) \(\def \PURPLE#1{{\color{purple} #1}}\) \(\def \th#1,#2{#1,\!#2}\) \(\def \lshift#1#2{\underset{\Leftarrow\atop{#2}}#1}}\) \(\def \rshift#1#2{\underset{\Rightarrow\atop{#2}}#1}}\) \(\def \dotspot{{\color{lightgray}{\circ}}}\) \(\def \ccw{\circlearrowleft}\) \(\def \cw{\circlearrowright}\)
Chapter 3: Linear Motion
12.

One-Dimensional Motion

When an object is moving along a straight line (that is, in one dimension) then we can express the object's displacement, velocity, and acceleration as a single number.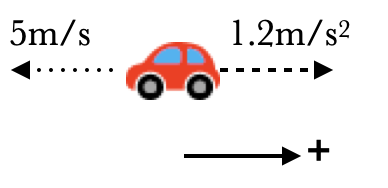

For example, consider a car with a velocity of "5m/s to the left" and an acceleration of "1.2m/s2 to the right". If we say that "to the right" is the positive direction, then we can write $\vec v=-5\u{m/s}$ and $\vec a=+1.2\u{m/s^2}$. Notice that the signs tell you the direction of the vector; in particular, the positive acceleration does not mean that the car is speeding up. To the contrary, because the velocity and acceleration point in different directions (and have opposite signs), we know that this car is slowing down.

What if we want to make leftward our positive direction? Then the velocity is $\vec v=+5\u{m/s}$ and $\vec a=-1.2\u{m/s^2}$.

The sign changes depending on our choice of what we call the positive direction, but the relative sign— the fact that the velocity and acceleration have opposite signs— remains the same, and the car"s behavior— that it is slowing down— also stays the same.