\(\def \u#1{\,\mathrm{#1}}\) \(\def \abs#1{\left|#1\right|}\) \(\def \ast{*}\) \(\def \deg{^{\circ}}\) \(\def \tau{\uptau}\) \(\def \ten#1{\times 10^{#1}}\) \(\def \redcancel#1{{\color{red}\cancel{#1}}}\) \(\def \BLUE#1{{\color{blue} #1}}\) \(\def \RED#1{{\color{red} #1}}\) \(\def \PURPLE#1{{\color{purple} #1}}\) \(\def \th#1,#2{#1,\!#2}\) \(\def \lshift#1#2{\underset{\Leftarrow\atop{#2}}#1}}\) \(\def \rshift#1#2{\underset{\Rightarrow\atop{#2}}#1}}\) \(\def \dotspot{{\color{lightgray}{\circ}}}\) \(\def \ccw{\circlearrowleft}\) \(\def \cw{\circlearrowright}\)
Chapter 8: Fluids
8.

Floating Objects

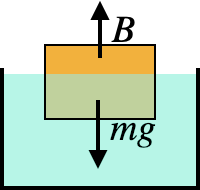
(no alternate text)

An object with a density less than that of water will rise to the surface, but once it gets to the top, of course it eventually comes to a stop. Why? Because as the object starts to leave the water, the buoyancy force starts to decrease, and becomes zero when the object is completely out of the water. Somewhere between “completely submerged” and “completely out of the water”, there’s a spot where the buoyancy force balances the force of gravity, and that’s the equilibrium point where the object will float.

The buoyancy of a floating object is

$$B=\rho_fV_{uw}g$$

with the portion of the object’s volume that is underwater. (Let’s call this $V_{uw}$, although the principle holds for all fluids, not just water.)

(no alternate text)

Push the floating object down into the water, and the portion $V_{uw}$ that is underwater will increase, and so the buoyancy force $B=\rho_fV_{uw}g$ will also increase. Raise the object up a little, and the buoyancy force will decrease. If we just place the object on the water and let it find equilibrium, then it will find the level where the buoyancy force balances the weight $mg$.

For a solid object with a consistent density $\rho_{\rm obj}$, like a block of wood, equilibrium is reached when $\rho_fgV_{uw}=(\rho_{\rm obj}V_{\rm obj})g$. Dividing both sides by $g$ gives us

$$\rho_fV_{uw}=\rho_{\rm obj}V_{\rm obj} \quad\hbox{ or }\quad {\rho_{\rm obj}\over \rho_f}={V_{uw}\over V_{\rm obj}}$$

That is, the fraction of the object that is underwater ($V_{uw}/V_{\rm obj}$) is equal to the ratio of the object’s density to the fluid’s density. For example, water ice has a density of 920kg/m3 while liquid water has a density of 1000kg/m3, and so $\rho_{\rm obj}/\rho_f=0.92$: 92% of floating ice lies under the surface of the water.