\(\def \u#1{\,\mathrm{#1}}\) \(\def \abs#1{\left|#1\right|}\) \(\def \ast{*}\) \(\def \deg{^{\circ}}\) \(\def \tau{\uptau}\) \(\def \ten#1{\times 10^{#1}}\) \(\def \redcancel#1{{\color{red}\cancel{#1}}}\) \(\def \BLUE#1{{\color{blue} #1}}\) \(\def \RED#1{{\color{red} #1}}\) \(\def \PURPLE#1{{\color{purple} #1}}\) \(\def \th#1,#2{#1,\!#2}\) \(\def \lshift#1#2{\underset{\Leftarrow\atop{#2}}#1}}\) \(\def \rshift#1#2{\underset{\Rightarrow\atop{#2}}#1}}\) \(\def \dotspot{{\color{lightgray}{\circ}}}\) \(\def \ccw{\circlearrowleft}\) \(\def \cw{\circlearrowright}\)
Chapter 8: Fluids
7.

Submerged Objects

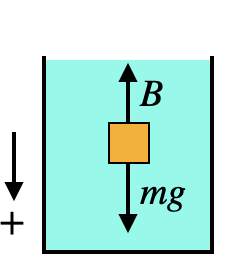
(no alternate text)

If an object is submerged in a fluid and released, the two forces acting on that object are buoyancy and weight. If we call downward the positive direction, then the net force on the object is $F_{net}=+mg-B$. If $\rho_{\rm obj}$ is the density of the object and the volume of the object is $V$, then $m=\rho_{\rm obj}V$. That means that $F_{net}=\rho_{\rm obj}Vg-\rho_fgV$, or $$\vec F_{net}=(\rho_{\rm obj}-\rho_f)Vg\downarrow.$$

If the object is more dense than the fluid so that $\rho_{\rm obj}-\rho_f>0$, then $\vec F_{net}$ points downward and the object will sink to the bottom, accelerating as it goes. For example, steel has a density of $\th8,000\u{kg/m^3}$ while water has a density of $\th1,000\u{kg/m^3}$, and so steel sinks in water. The larger the density, the larger the force and the faster it sinks.

If the object is less dense so that $\rho_{\rm obj}-\rho_f<0$, then the net force is upward and the object will float towards the surface, accelerating on the way. Less dense objects have a larger acceleration and rise more quickly. For example, styrofoam has a density of $50\u{kg/m^3}$, and so $0.001\u{m^3}$ of styrofoam in water feels a force of $-9.31\u{N}$, and an acceleration of $380\u{m/s^2}$!

Remember that whether something floats or sinks depends also on the density of the fluid it is in: mercury has a density of $\th13,500\u{kg/m^3}$, and so steel will float on mercury even though it sinks in water.

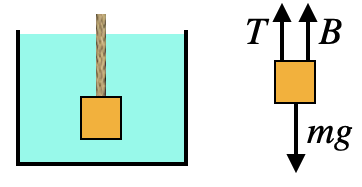
If other objects are touching the block, draw a force diagram including the buoyancy force, and solve.

This all assumes that there is nothing touching the object other than the fluid. If the object is suspended or held down, then one can draw a force diagram, with buoyancy being treated as one of the forces.