Boats and Balloons

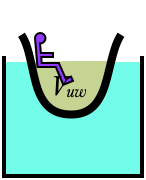
A boat can float on water, even when made of a high-density object like iron, because it is designed to displace more water than a solid object would. As people and cargo are loaded onto the boat, it rides lower in the water, which increases the fraction of the boat which is underwater, which in turn increases the buoyancy force $B={\rho }_f{V}_{uw}g$: this increased buoyancy force is enough to support the additional weight. The buoyancy force can continue to increase until the entire boat is submerged and $V=V_{uw}$ (or else if water is able to spill into the boat, increasing its weight further.)

All fluids exert a buoyancy force on the objects inside it. Air, for example, exerts an upward force of $B={\rho }_f{V}_{\mathrm{o}\mathrm{b}\mathrm{j}}g$ on everything inside the air with volume $V_{\mathrm{o}\mathrm{b}\mathrm{j}}$. For example, a human has an average volume of $0.06{\mathrm{m}}^3$, and since the atmosphere has a density of ${\rho }_f=1.2\mathrm{kg}/{\mathrm{m}}^3$, it exerts an upward force of about $B=(1.2)(0.06)(9.8)=0.7\mathrm{N}$ on the average human. In other words, even though most of the atmosphere is above you, it is actually lifting you up, making you a little lighter than you would be otherwise.

A helium balloon floats upward because the density of helium is much less than the density of the atmosphere. For example, a spherical balloon with a radius of 0.15m has a volume of $V=\frac{4}{3}\pi r^3=0.014{\mathrm{m}}^3$, and feels a force of 0.16N. If the balloon has a weight less than 0.16N (or a mass of 16 grams), including the rubber and the helium, will float into the air.

Hot air balloons work under the same principle, with the added fact that the air inside the balloon expands as it warms up, and thus has a lower density. Hot air has the advantage over helium in being much more common (the world is facing a helium shortage right now) and easier to control by changing the temperature of the air.