Flow Rate

Its SI units are cubic meters per second, although this is a very large flow; a more practical unit is the liter per second: $$1\frac{{\mathrm{m}}^3}{\mathrm{s}}=1000\frac{\mathrm{L}}{\mathrm{s}}$$

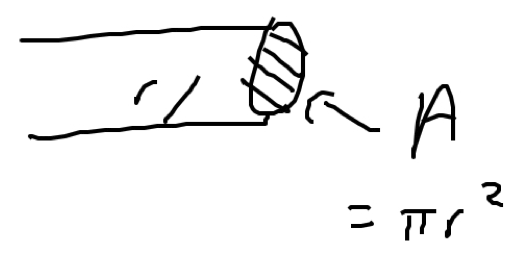
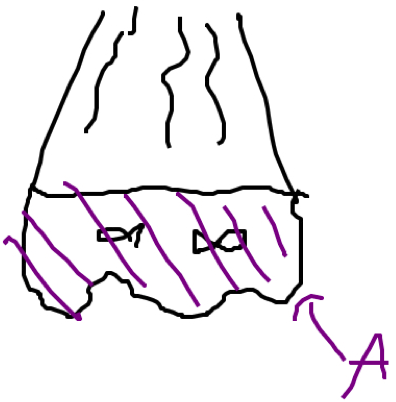
The flow rate through a pipe (or channel, or river, or whatever) depends on two things: how big the pipe is (bigger pipes mean greater flow) and how fast the water runs through the pipe. In fact, the flow rate can be found using the formula

where $v$ is the speed of the water, and $A$ is the cross-sectional area of the pipe.

When the fluid is a liquid, so that its volume remains constant, then the total flow rate into an object (a pipe, a box, whatever) must be equal to the total flow rate out of the object: if not, then either there will be a buildup of fluid inside the object (if ${\mathrm{\Phi }}_{\mathrm{i}\mathrm{n}}$ is bigger) or there would have to be a secret cache of fluid inside the object which is being depleted (if ${\mathrm{\Phi }}_{\mathrm{o}\mathrm{u}\mathrm{t}}$ is bigger). In either case, the situation would not be able to go on for very long. In the case of steady flow, then, or flow which lasts for a long time, we must have $${\mathrm{\Phi }}_{\mathrm{i}\mathrm{n}}={\mathrm{\Phi }}_{\mathrm{o}\mathrm{u}\mathrm{t}}$$

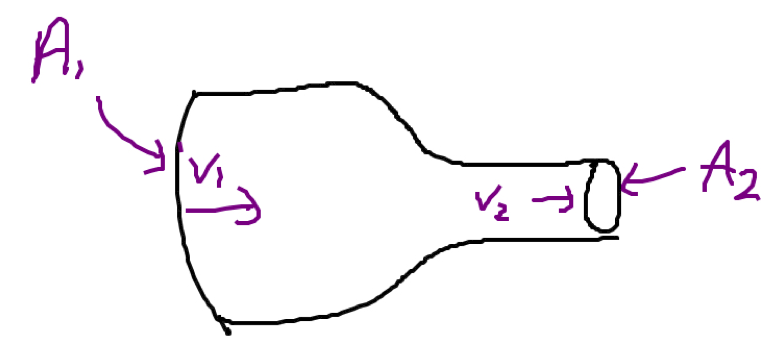
For example, if water flows through a pipe that changes diameter, then we can write $$A_1{v}_1=A_2{v}_2$$ If the pipe gets narrower, so that $A_1>A_2$, then the final speed $v_2$ must be greater than the initial speed $v_1$ in order to compensate for the smaller area. Water speeds up when the pipe narrows (picture a hose when you place a finger over the end) and slows down when the pipe (or a river) widens (such as a river which goes from narrow rapids to become wider, deeper, and calmer later on).