Torque Direction

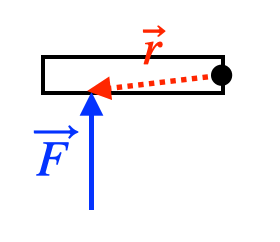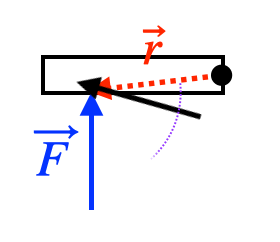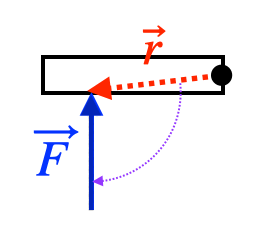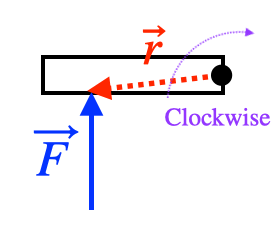
Objects that spin in a circle can spin in two different directions, clockwise ( $↻$ ) and counterclockwise ( $↺$ ), and therefore torques can point in both directions as well. Sometimes you can figure out the direction of a force's torque by just looking at the object and imagining how that force would spin the object if it were allowed to. But if you want something more solid, you can use this technique:

The direction of the torque is the direction you need to turn

\vec{r}

so that it points in the direction of

\vec{F}

. If

\vec{r}

points in the same (or opposite) direction as

\vec{F}

, then the torque is zero.

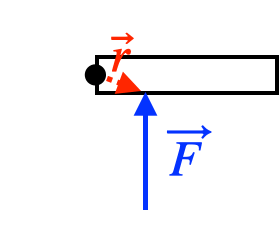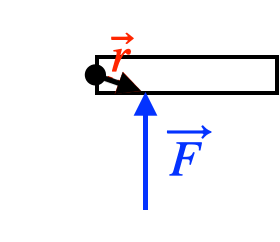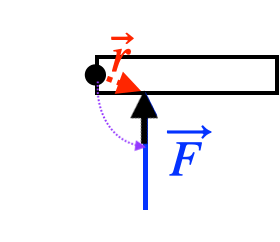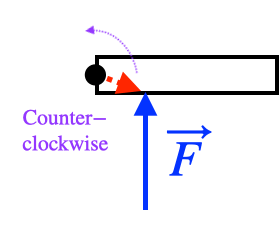
Note that the direction of the torque can change if the location of the pivot changes, even though the force stays the same.

Quiz

Use this quiz to practice determining the direction of a torque.