Torque

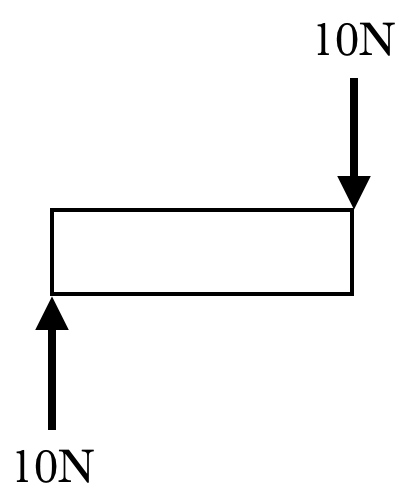
Torque

$\tau$

Units:N m

Sometimes it's not enough for the forces to balance. For example, suppose two equal forces were applied on the box as shown here. If you tried this yourself, you would see that the box will rotate clockwise. The tendency of a force to cause an object to rotate around a particular axis or pivot is called torque.

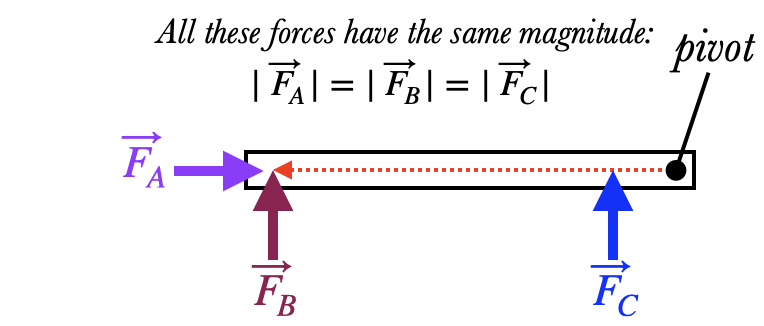
Torque depends not only on how strong the force is, but also where and how the force is applied relative to the pivot. For example, in this figure

the torque due to $\vec F_B$ is larger than the torque due to $\vec F_C$, because it is easier to open a door when you push on the side that is opposite the hinges.
On the other hand, $\vec F_A$ exerts no torque at all, because if you push on the edge of the door directly towards the hinges then you won't make it spin at all, no matter how hard you push.

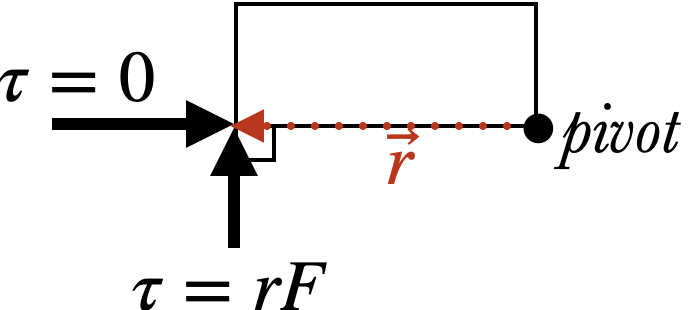
When calculating the torque, we specify the location of the force with the lever arm vector $\vec r$, which is the vector from the pivot to the place where the force is being applied. If $r$ is the length of the lever arm and $\theta$ is the the angle between the force and its lever arm, then the torque $\tau$ of $\vec F$ around that pivot is

$$\tau=rF\sin\theta$$

The units of torque are the length of the lever arm times the magnitude of the force; thus Newton-meters (Nm). The sine is a measure of "how perpendicular" the two vectors are, and there are two cases which are worth singling out:

If the force points directly towards or away from the pivot (so that $\vec F$ and $\vec r$ are parallel), then $\sin\theta=0$, and the torque is zero as well.
If the force is perpendicular to the lever arm, then $\sin\theta=1$, and we have $$\tau = rF \hbox{ (if } \vec r\perp\vec F\hbox{)}$$

Footnote

Note that we use the lowercase Greek letter $\tau$ for torque; be sure to distinguish it from a lower-case $t$ or upper-case $T$. See The Greek Alphabet for a suggestion of how to write the letter distinctly.