12.
The Breaking of Static Friction
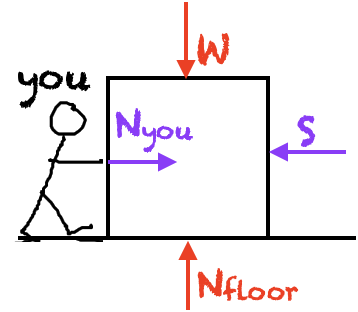
Consider that box you were trying to push across the floor in Static Friction. You ask a friend to help, and together you can push really hard, and suddenly the box starts moving. Your push gets so large that the static frictional force cannot become large enough to balance it anymore, and so the friction "breaks" and completely disappears, the way a rope might break. In other words, static friction has a maximum value.
Coefficient of static friction
\(\mu_S\)
--- how slippery the surfaces are. This is described by a number \(\mu_S\) called the coefficient of static friction. The larger this coefficient is, the harder it is to break the static friction. (See Coefficients of Friction for some example values.)
- how hard the surfaces are pressed together; that is, the size of the normal force \(N\) of one surface on the other.
Accepting this model as true, we write
$$S\le \mu_SN$$
Example
This breaking is probably something you’ve noticed before. Put your hand against the top of a table and very gently pull your hand back without causing your hand to slide. The moment your hand starts to move is when the static friction breaks. Now press down hard on your hand with your other hand, and try the same thing. Notice that the static friction lasts a lot longer this time!It is important to remember that \(\mu_SN\) is not the static frictional force itself; the static friction is an adjustable force and it doesn't have a formula. This is just the maximum value the force can have before it breaks.