Pendulum

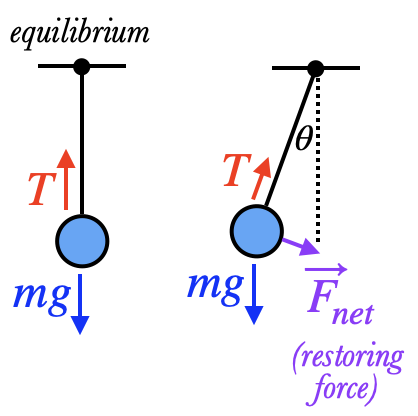
A mass suspended from a string and allowed to swing is called a pendulum. There are two forces acting on the mass (or "bob"): its weight, and the tension from the string. When the string is vertical, the two forces cancel and the pendulum is in equilibrium. If the pendulum is pulled to one side, however, the net force of weight and tension on the mass pulls the pendulum back towards the center, acting as a restoring force and causing oscillation. (It may be more accurate to talk about the weight exerting a restoring Torque on the pendulum, since the pendulum is moving along an arc.)

If the displacement angle of the pendulum remains small ($\theta<20^\circ$ or so), then the period and frequency of the pendulum is approximately $$T=2\pi\sqrt{L\over g} \qquad f=\frac1{2\pi}\sqrt{g\over L}$$ where $L$ is the length of the string and $g=9.8\u{kg/m^2}$ is our old friend. Longer pendula have longer periods, and take longer to swing back and forth.

What's particularly interesting about a pendulum's frequency is what it doesn't depend on: the mass of the bob, or the angle of the string. This makes a pendulum a particularly good clock: we can measure the length of the pendulum fairly precisely, and we do not have to worry about the bob collecting dust, or about how far back we start it swinging.