Block on a Spring
Earlier in the book we talked about the force that a spring will exert on an object. When a spring is relaxed, it exerts no forces at all, and we call its relaxation length $L_0$. When the spring is stretched to a larger length $L>L_0$, then it pulls back with a force $$F=k\abs{L-L_0}$$ in an attempt to restore itself to its relaxation length. The farther the spring is stretched, the harder it pulls back. The reverse occurs when the spring is compressed to a shorter length $L
The amplitude of this oscillation depends on how far back you pull the block before you let it go. The period and frequency of this oscillation depends on the mass of the block and the stiffness of the spring:
A stiffer spring results in a "faster" (i.e. more frequent) oscillation, while a larger mass (more inertia) results in a "slower" (less frequent) oscillation.
A block which hangs from a vertical spring is a little more complicated, because now there is the force of gravity to attend to. The equilibrium point of the spring isn't where the spring is relaxed, but where the spring force balances the force of gravity: $$k(L-L_0) = mg \implies L_{eq} = L_0 + {mg\over k}$$
Div
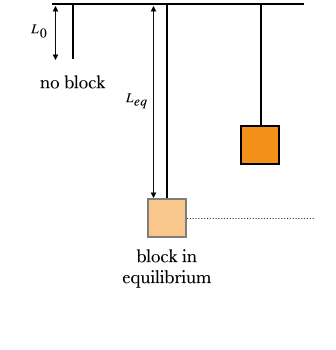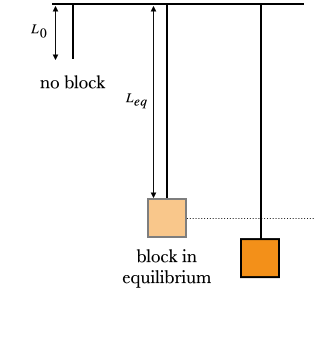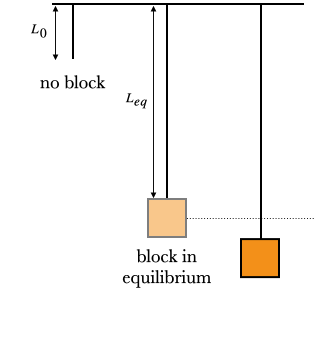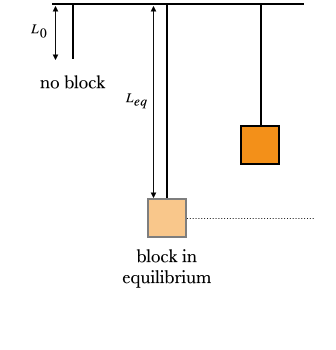
When the block falls below this equilibrium point, the force of the spring is greater than the weight of the block, and so the net force is upward, back towards the equilibrium point. If the block rises above the equilibrium point, then the spring force, while still pointing upward, is smaller than the weight, and so the net force points down. In other words, the spring force and the weight combine to form a restoring force which brings the mass back to its equilibrium point, and so this block oscillates as well. And even better, the period and frequency formulas are the same as those of the horizontal block. This is good, because this is a much easier experiment to set up.