Simple Harmonic Motion

When the restoring force on an oscillating object is proportional to its displacement (that is, when $F\sim y(t)$), then the oscillation is called simple harmonic motion. If we graph the displacement of such an oscillation as a function of time, we find that the displacement is sinusoidal-- it looks like a sine or cosine function.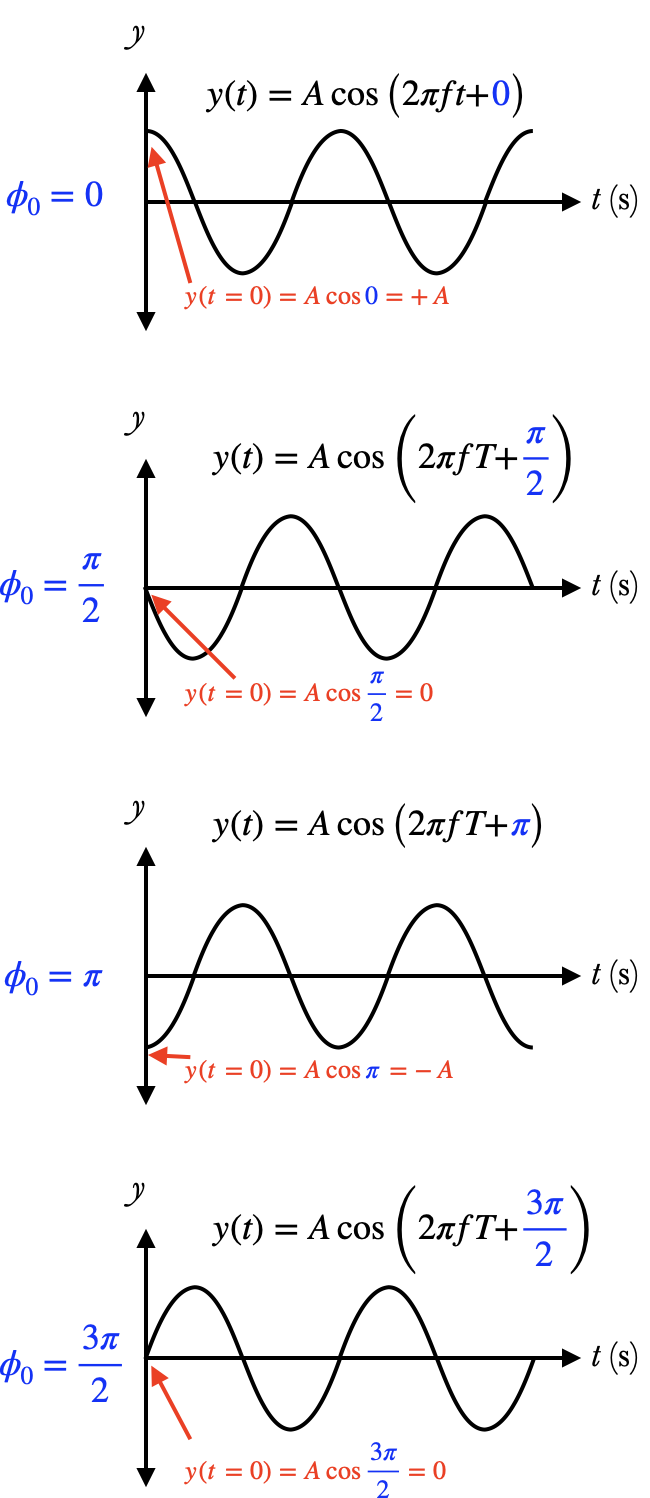

We can write the displacement as a cosine (in radians mode):

$$y(t) = A\cos\left(2\pi {t\over T}+\phi_0\right)$$

where

$A$ is the amplitude of the oscillation
$T$ is the period of the oscillation
$\phi_0$ is a number called the initial phase, which depends on where in the cycle the oscillation is at $t=0$. Most times we'll assume that $\phi_0=0$ for simplicity.

For example, if $\phi_0=0$, then $$y(t=0) = A\cos \left(2\pi {0\over T}\right) = A\cos 0 = A$$ because $\cos 0=1$ (see Trigonometric Functions). At $t=T$, it will have completed exactly one cycle, and its displacement is now $$y(t=T)=A\cos\left(2\pi {T\over T}\right) =A\cos 2\pi = A$$ because $\cos2\pi = 1$. (We must work with radians in this section!)

Because $f=\frac1T$, we can also write the displacement as

$$y(t) = A\cos\left(2\pi ft+\phi_0\right)$$

Physicists like this version because we don't like writing fractions if we can avoid it.