Temperature

Some Useful Temperatures

Reference	Celsius	Kelvin	Fahrenheit
absolute zero	-273°C	0K	-459°F
water freezes	0°C	273K	32°F
an autumn day	10°C	283K	50°F
room temperature	20°C	293K	68°F
warm summer day	30°C	303K	86°F
body temperature	37°C	310K	99°F
water boils	100°C	373K	212°F

You probably have an intuitive grasp of what temperature is already: hotter objects have higher temperatures than colder objects. At the microscopic level, temperature is the measure of the amount of random energy the atoms and molecules of a material have: as the temperature rises, the molecules in an object begin to vibrate (or in a fluid, rotate and wander about) more quickly. Temperature is related to thermal energy, except thermal energy also depends on size (a ton of bricks will have more thermal energy than a single brick with the same temperature) and material (water holds more thermal energy than iron, for instance).

$$\begin{align} {}^\circ C&={5\over 9}({}^\circ F-32)\\ {}^\circ F&={9\over 5}{}^\circ C+32\\ {}^\circ C&=K+273\\ \end{align}$$

In everyday life, people measure temperature in one of two scales: the Fahrenheit and the Celsius scale. You can convert between one and the other using the formulas shown here.

Temperature

$T$

Units:K

While Celsius is often considered the “metric system” temperature scale, in fact neither Celsius and Fahrenheit are ideal for physicists. In physics, when we say that a quantity is zero, that means that nothing is going on: that there is a complete lack of something (force, speed, acceleration, whatever). But an ice cube at 0°C (the freezing point of water) doesn't "lack temperature". Molecules still vibrate inside a block of ice. And there’s nothing qualitatively different between a negative temperature and a positive except that the former is colder: an object which is –10°C is also +14°F, for instance.

The official SI unit of temperature is called the kelvin, and it is an absolute temperature scale: this means that the molecules in an object with a temperature of 0K (which is called absolute zero) have no thermal energy: they do not vibrate or rotate or wander at all. Absolute zero in Celsius is –273°C, so we can convert from Kelvin to Celsius by adding 273, and convert back by subtracting.

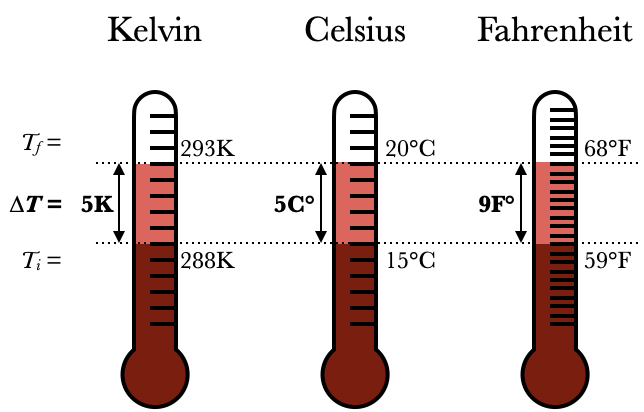
The Kelvin scale is defined so that the size of a Kelvin degree is equal to the size of a Celsius degree: that is, the distance between tics on the two thermometers are the same. (See the picture on the right.) This means that changes in temperature °T have the same value in Celsius and Kelvin, and even though individual temperatures are not. For instance, the thermometers on the right show an increase in temperature from 15°C to 20°C, which is also an increase in temperature from 288K to 293K. But both thermometers show an increase of 5. To make the distinction, we write 5°C ("five degrees Celsius") to indicate a specific temperature on the thermometer, but 5C° ("five Celsius degrees") to indicate a change in temperature. Note that $5\u{C\deg} = 5\u{K}$ (same $\Delta T$) but $5\u{\deg C} \ne 5\u{K}$ (different $T$).

(Fahrenheit has a smaller spacing in between its degrees, so a change of 5C° corresponds to 9F°)

As a rule of thumb:

When a physics equation contains a $T$, use Kelvin.
When a physics equation contains a $\Delta T$, you may use either Kelvin or Celsius.