Linear & Angular Motion

When you sit on a spinning merry-go-round, not only are you spinning around its axis, you are also moving through space: you have both a linear velocity v as well as an angular velocity $\omega$. The two quantities are related: the faster * the merry-go-round spins, the greater your linear velocity. Let's see how.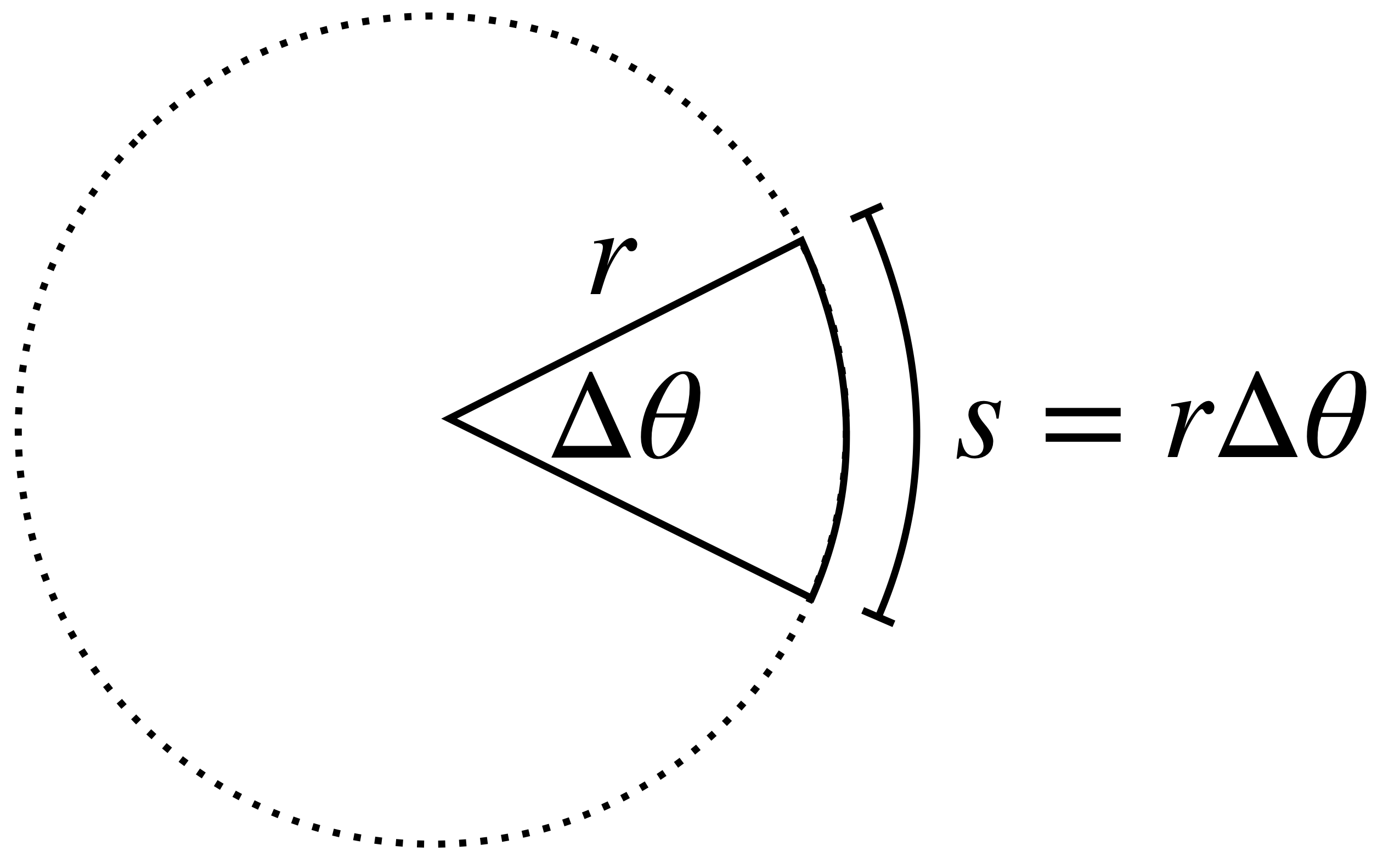

We've mentioned how much mathematicians and physicists love to measure angles in radians, but at first glance it seems like a weird choice: why should one complete revolution be equal to 6.2831853... radians? Why bring $\pi$ into it? The reason is this: if you consider a portion (or "arc") of a circle with radius $r$, and the arc spans an angle $\Delta\theta$, then the length $s$ of the arc is

$$s=r\Delta\theta$$ <i>only</i> if $\Delta\theta$ is in radians

Example

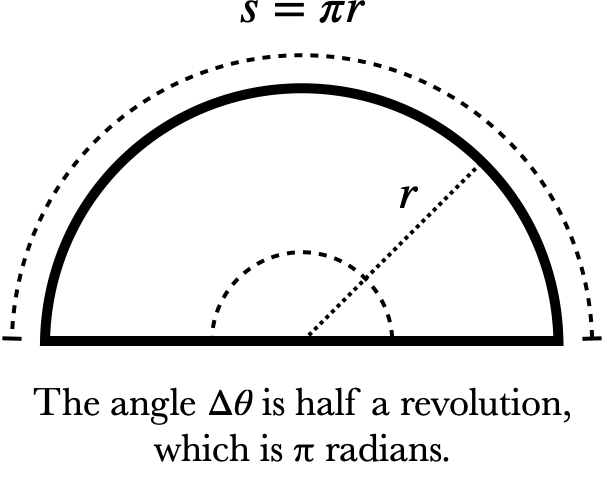
Consider a semicircle with radius $r$. It spans half a complete revolution, and so its angle is $\Delta\theta=\frac12(2\pi)=\pi$. The length of the semicircle is thus $s=r\Delta\theta=r\pi$. Since the circumference of a full circle is $2\pi r$, it makes sense that the length of a semicircle is half of that. Obviously this wouldn't work in degrees: the length of the semicircle can't be $3.14159r$ and $180r$ at the same time!

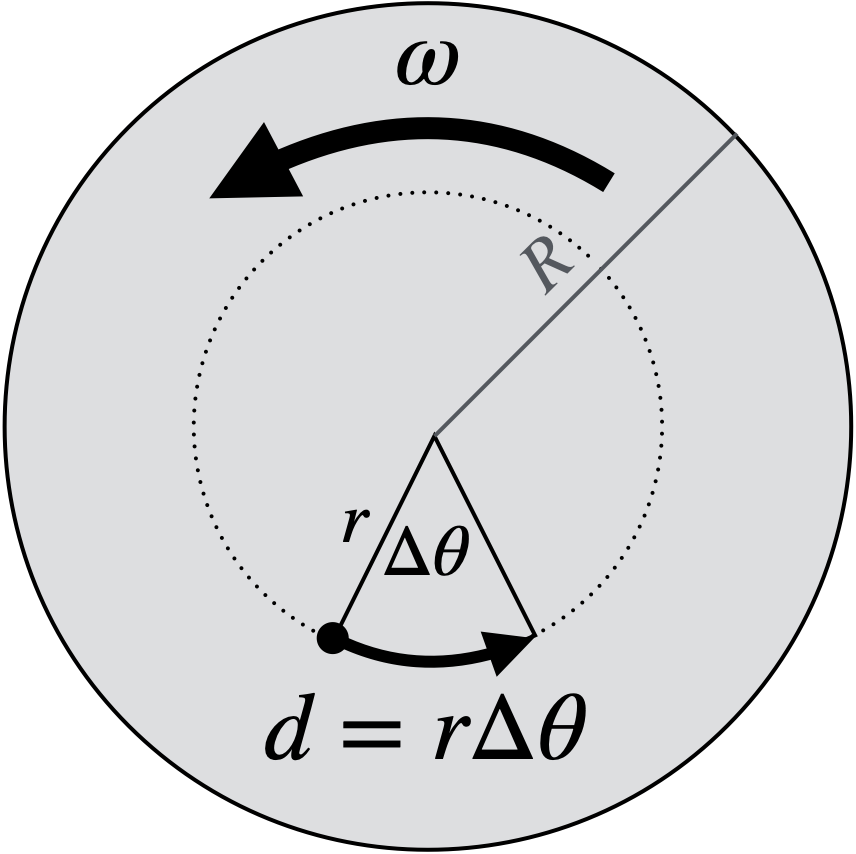
Now consider a wheel that is spinning with a constant angular velocity $\omega$ counterclockwise, and think about a point on that wheel which is a distance $r$ from the center. If the wheel spins for a certain time $\Delta t$, then the point will travel through an angle $\Delta\theta=\omega\Delta t$ according to the definition of Angular Velocity. Because the point is moving in a circle with radius $r$, it thus travels a distance $d=r\Delta\theta = r(\omega\Delta t)$ in time $\Delta t$, and so the point's linear velocity is $$v={\text{distance}\over\text{time}}={d\over\Delta t}={r\omega\Delta t\over\Delta t}$$

$v=r\omega$ (where $\omega$ is in rad/s)

Points farther from the center of the wheel move with a higher speed than points closer to the center. The velocity is always tangent to the circular path the point is travelling at any given moment.

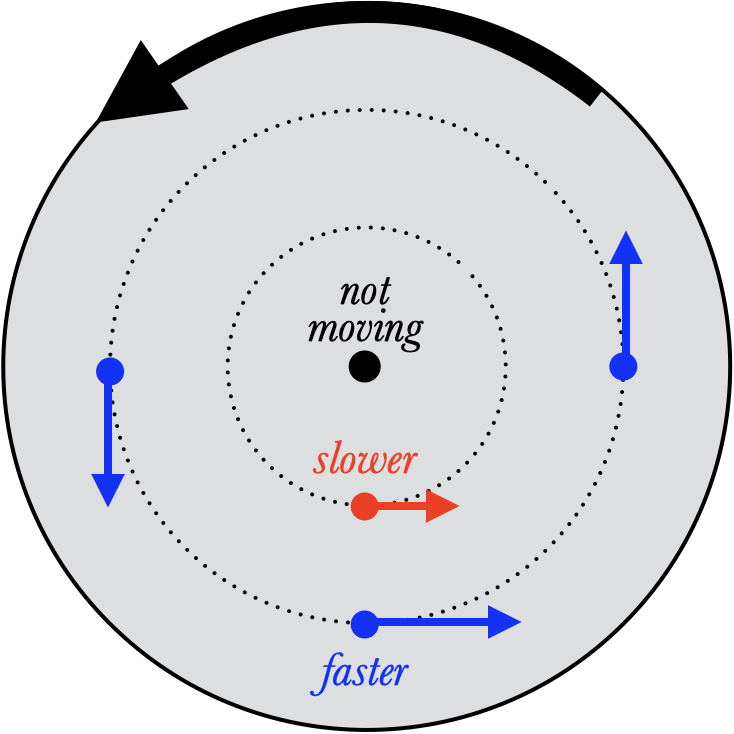
Notice that the $r$ is the distance of the relevant point from the axis, not the radius of the wheel itself. Different points on the wheel move at different speeds: the point farthest from the axis moves the fastest, while the center doesn't move at all (because $r=0$ there).

Linear and angular acceleration are also related, but the connection between them is a little more complicated. Remember that the velocity of an object in Uniform Circular Motion is always perpendicular to the radius: even if the speed is constant, the velocity is always changing direction, and so it always has a linear acceleration $a_c=\frac{v^2}{r}$ towards the center of the circle: the "$a_c$" stands for centripetal acceleration because it points towards the center. If the object starts spinning more quickly, however, then the object will also have a tangential acceleration $a_t$ which points in the same direction as the object's velocity; conversely, $a_t$ points in the opposite direction of the velocity if the spin is slowing down. The tangential acceleration is related to the angular acceleration:

$a_t=r\alpha$ (where $\alpha$ is in $\u{rad/s^2}$)

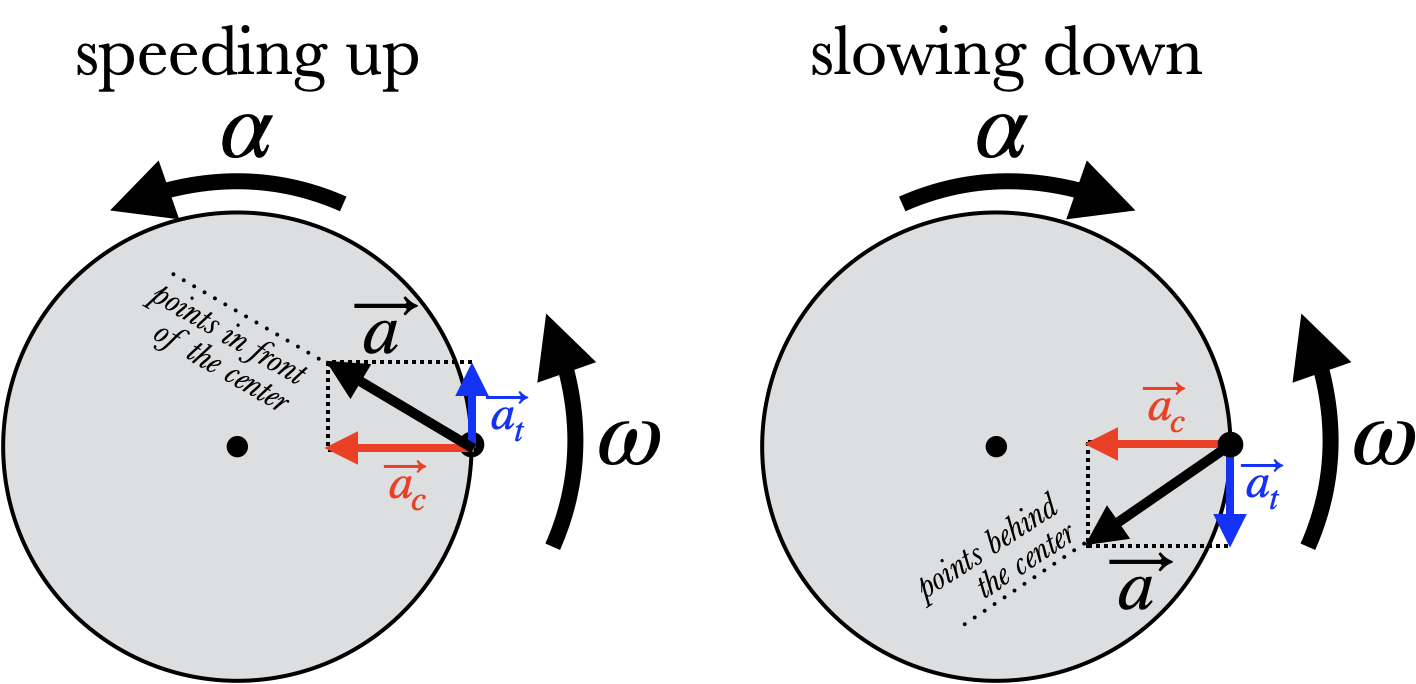
The total acceleration of the object is the sum of these two quantities as vectors:

$$\vec a=\vec a_c+\vec a_t \qquad a=\sqrt{a_c^2+a_t^2}$$

The acceleration will always point towards the center, more or less, but if the object is speeding up, then the acceleration vector points ahead of the center; while it points behind the center if the object is slowing down (as is shown in the figure).

Footnote

The words "faster" and "slower" can be confusing in this context, since they might refer to linear or angular velocity: we say that a wheel is spinning faster if its angular velocity increases, but we can also say that one point on the wheel moves faster (has a larger linear velocity) than another even though both are spinning at the same rate. This text will do its best to make the use of the words "faster" and "slower" clear, but you should read carefully whenever the words appear in the context of something that is spinning.