4.
Transmission of Light
When light passes from one material to another, it usually changes speed. Because light is a wave, it obeys the wave equation $v=\lambda f$, so only the wavelength or the frequency can stay the same in both materials; the other one must change. We will show that the frequency must stay the same in both materials. If the wavelength stayed the same, then the frequency would increase as the speed increases. But consider the point on the interface, which belongs to both materials: is it oscillating according to the freuqency on the left, or the right? Notice in the animation how sometimes it needs to be a crest AND a trough at the same time. This isn't possible. When the frequency stays the same, on the other hand, we don't have those contradictions.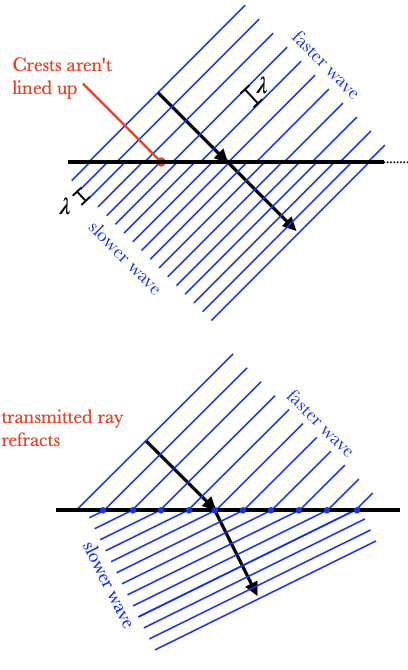
If light waves travel along the normal of an interface, then this change isn't visible. If the light ray comes in from an angle, however, we have a new problem. If the ray keeps moving in the same direction, then the wavefronts don't line up at the interface, and we get the same problem: a point on the interface would have to be a crest and a trough at the same time. The only way the wavefronts can line up is if the ray bends, or refracts, as it enters the new medium.