Law of Reflection
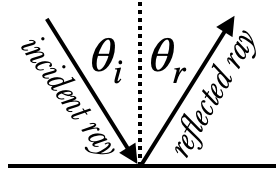
This picture shows a ray of light reflected from a surface. The incident ray makes an angle of $\theta_i$ with the normal, and the reflected ray makes an angle of $\theta_r$ with the normal. The two angles are related by a very simple equation:
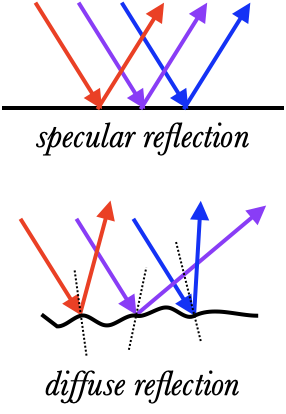
The one tricky bit about this is noting that the normal is perpendicular to the surface at the place the ray hits. If the surface is perfectly flat, then parallel rays which hit the surface at one angle all reflect in the same direction. This is called specular reflection. If those incident rays are from an object, then someone who sees the reflected rays will also be able to see that object as if they were looking directly at it.
From a curved or bumpy surface, parallel rays will be reflected in all different directions. This is called diffuse reflection, and it is what happens when light hits most surfaces: even if they appear smooth, there are usually small irregularities in the surface which causes light to scatter. Only from perfectly flat surfaces like the back of a mirror, or the surface of a calm pond, does specular reflection occur.