\(\def \u#1{\,\mathrm{#1}}\) \(\def \abs#1{\left|#1\right|}\) \(\def \ast{*}\) \(\def \deg{^{\circ}}\) \(\def \tau{\uptau}\) \(\def \ten#1{\times 10^{#1}}\) \(\def \redcancel#1{{\color{red}\cancel{#1}}}\) \(\def \BLUE#1{{\color{blue} #1}}\) \(\def \RED#1{{\color{red} #1}}\) \(\def \PURPLE#1{{\color{purple} #1}}\) \(\def \th#1,#2{#1,\!#2}\) \(\def \lshift#1#2{\underset{\Leftarrow\atop{#2}}#1}}\) \(\def \rshift#1#2{\underset{\Rightarrow\atop{#2}}#1}}\) \(\def \dotspot{{\color{lightgray}{\circ}}}\) \(\def \ccw{\circlearrowleft}\) \(\def \cw{\circlearrowright}\)
Chapter 5: Impulse and Momentum
4.

Total Momentum

One important distinction between velocity and momentum is that the total momentum of a system— the sum of the momenta of various parts of a system— is meaningful, while the total velocity does not.

For example, consider a 12kg block sitting on top of a 20kg block. Both are moving at 4m/s in the positive direction. The momenta of the two blocks is $\RED{\vec p_{top} = +48\mathrm{Ns}}$ and $\BLUE{\vec p_{bottom} = +80\mathrm{Ns}}$. Now suppose we think of the two blocks as a single object (which we will call a system) with a mass of $12+20=32\u{kg}$, as if they were glued together. The momentum of that object would be $\PURPLE{\vec p_{both}=(32\mathrm{kg})(+4\mathrm{m/s})=+128\mathrm{Ns}}$, and a little math shows us that $\RED{\vec p_{top}}+\BLUE{\vec p_{bottom}}=\PURPLE{\vec p_{both}}$. This is true in general:

Note

Note that this is not true for velocities: the "total velocity" of these two blocks, 8m/s, has no particular meaning at all.
The momentum of a system of objects is equal to
the sum of the momenta of its individual components.

This may seem like an obvious statement, but here's a neat trick: "systems of objects" can include objects that aren't stuck together, and we can talk about the total momentum of objects even if if they're moving in different directions, different speeds, or even if they have nothing to do with each other. For example, the total momentum of these two blocks

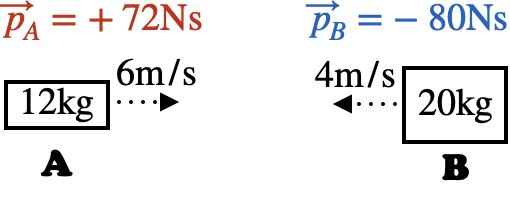
is $(72\u{Ns})+(-80\u{Ns})=-8\u{Ns}$, or $8\u{Ns}$ to the left. We will see the significance of this, and the power of this concept, in Conservation of Momentum.