Conservation of Momentum
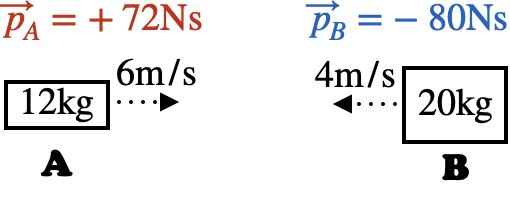

Think back to our two collisions in Total Momentum, hurtling towards each other. Call them $\RED{A}$ and $\BLUE{B}$. Once they collide, block A will exert a force $\BLUE{\vec F_{A\to B}}$ on B, and block B will exert a force $\RED{\vec F_{B\to A}}$ on A.
Because of Newton's Third Law, these two forces are equal in magnitude and opposite in direction: $\RED{\vec F_{B\to A}}=-\BLUE{\vec F_{A\to B}}$, and so their impulses must also be equal and opposite: $\RED{\vec J_A}=-\BLUE{\vec J_B}$.
We can find the total impulse on the system of both blocks by adding the impulses on each block individually: $$\vec J_{total}=\RED{\vec J_A} + \BLUE{\vec J_B}=0$$ (There are other impulses on both blocks, from gravity, friction, and so on, but as mentioned in Bouncing Off Walls these are small during a collision and can be ignored.) Since $\Delta \vec p_{total}=\vec J_{total}$, the change in the total momentum must be zero during the collision. This is a general result that can be applied to collisions that happen over a short period of time, and is called conservation of momentum.
system of the objects involved stays the same.
Notice what this statement does not say:
- The momenta of the individual blocks can and will change during the collision (they will end up moving in opposite directions, for one thing): it's only the total that stays the same.
- The total momentum is only conserved during the collision itself. For example, after the collision the two blocks may come to a stop due to friction, reducing their total momentum to zero. This is after the collision, but not immediately after the collision.
With those caveats in mind, momentum is still a powerful tool when analyzing collisions: it lets us ignore all the ugly details of the collision itself, and determine what happens right after the collision based on what was happening right before.
Momentum isn't enough to make a complete prediction about what the blocks will do, but it does limit the range of possibilities. All three of these could be pictures of what the blocks do immediately after the collision: what they all have in common is that their total momentum is –8Ns, the same as it was before the collision.
