Trigonometric Functions

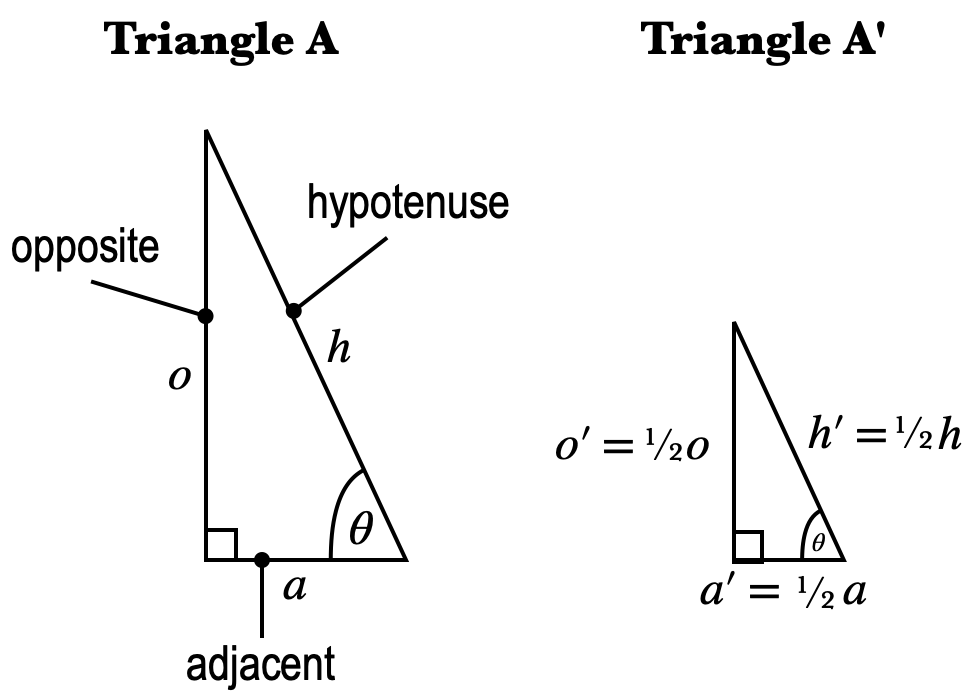
You may remember from geometry that if you take a triangle and then shrink down all its sides by the same fraction (as you might on a photocopier), then the resulting triangle will have the same angles as the original triangle. We say that these two triangles are similar. For example, the two triangles shown in the figure here are similar right triangles; the angle $\theta$ is the same on both. If we calculate the ratios of the opposite side to the hypotenuse, we'll find that the ratios are the same for both triangles: $${o'\over h'}={{\redcancel{1/2}}\,o\over {\redcancel{1/2}}\,h}={o\over h}$$ The same is true for the ratios of any two matching pairs of sides. This is true for any two right triangles with the same angle $\theta$, and being rather universal and handy, these trigonometric ratios are given special names:

SINE

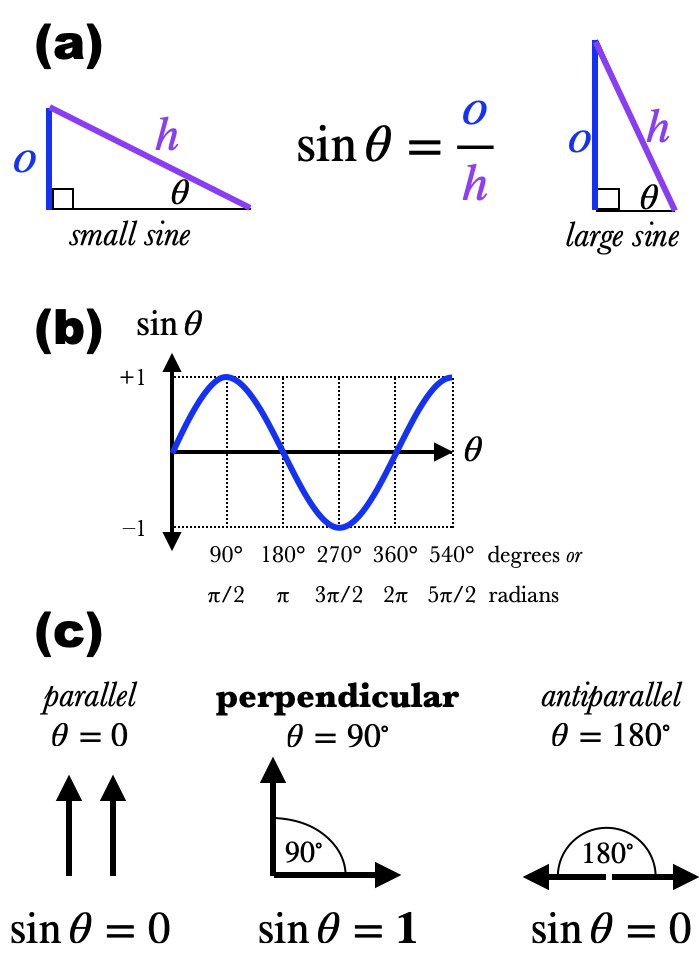
The sine is the ratio of the side opposite of the angle $\theta$ to the hypotenuse: $$\sin\theta = {o\over h}$$ As the angle gets bigger, $o$ gets bigger (as shown in Figure (a)), and so the sine gets bigger as well, between the limits $$\begin{align} \sin 0\deg &= 0\\ \sin 90\deg &= 1 \qquad \text{ (or $\sin{\pi \over 2} = 1$ in radians)}\\ \end{align} $$ The sine is also defined for angles larger than 90° as well, alternating between -1 and 1. For example, $$\sin 180\deg=0\qquad\sin 270\deg=-1\qquad \sin 360\deg=0$$ The graph of the sine is a periodic function called the sine wave, as seen in Figure (b)).

The sine is often used as a measure of how perpendicular two vectors are (as shown in Figure (c)). If the angle between two vectors is $\theta$ and they are pointing in the same direction ($\theta=0\deg$) or in opposite directions ($\theta=180\deg$), then $\sin\theta = 0$. If two vectors are perpendicular to each other ($\theta=90\deg$), then $\sin\theta =1$.

COSINE

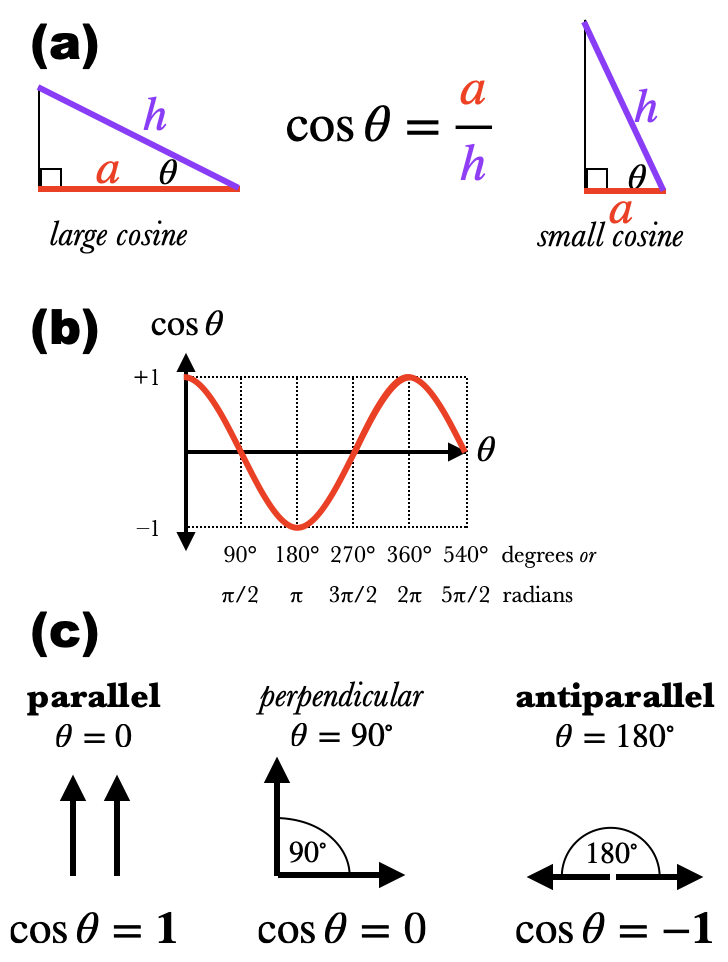
The cosine is the ratio of the side adjacent to the angle $\theta$ and the hypotenuse: $$\cos\theta = {a\over h}$$ As the angle $\theta$ gets bigger, the cosine gets smaller, between the limits $$\begin{align} \cos 0\deg &= 1\\ \cos 90\deg &= 0 \qquad \text{ (or $\cos{\pi\over 2}=0$ in radians)}\\ \end{align} $$ Like the sine, the cosine can also be defined for other angles, and is always between -1 and 1: $$\cos 180\deg=-1\qquad\cos 270\deg=0\qquad \sin 360\deg=1$$ The graph of the cosine is a periodic function called the cosine wave, and is identical to the sine wave except it is shifted over so that it starts high at $\theta=0$.

Leftnote

There's a useful mnemonic to remember the difference between sine and cosine: the co- in cosine means "together" (or you can think "co as in cozy" if you want). Thus a cosine is a measure of how much two vectors "go together" (i.e. point in the same direction). It is also a reminder that the cosine depends on the adjacent side (the one that is "together" with the angle), not the opposite side.

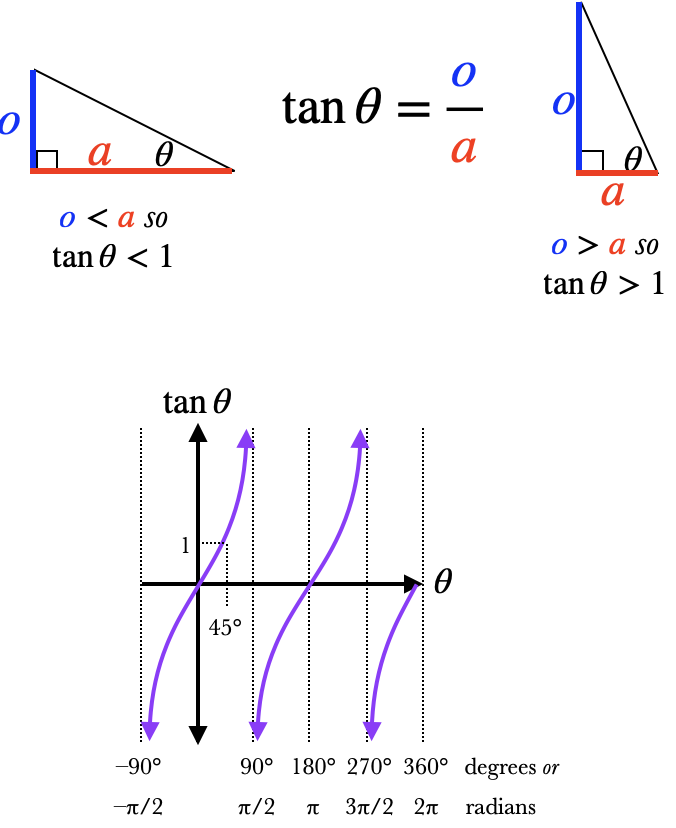
The cosine is a measure of how parallel two vectors are (as shown in Figure (c)). If two vectors are pointing in the same direction ($\theta=0$), then the cosine is 1, because that's as parallel as they get. When they are perpendicular, then they're not parallel at all, and so the cosine is 0. If the vectors point in opposite directions ($\theta=180\deg$), we say they are antiparallel, and their cosine is -1. The cosine is positive if the vectors are roughly pointing in the same direction, and negative if they are pointing in roughly opposite directions.

TANGENT

In a right triangle, the tangent of an angle is the ratio of the opposite side over the adjacent side: $$\tan\theta = {o\over a}$$ Because $\sin\theta = o/h$ and $\cos\theta=a/h$, we can show that $$\tan\theta = {\sin\theta\over \cos \theta}$$ When $\theta$ is small, the opposite side will be smaller than the adjacent side, and so $\tan\theta<1$; when $\theta$ is big, the opposite side is bigger, and $\tan\theta>1$. The two sides are of an equal length when $\theta=45\deg$ (when we have an isosceles triangle), and so $\tan45\deg=1$. (From this it follows that $\sin45\deg=\cos45\deg$ too; they both equal $1\over\sqrt2$.)

The tangent function isn't stuck between -1 and 1; it can have any value between $-\infty$ and $\infty$, as shown in the graph.

SMALL ANGLES

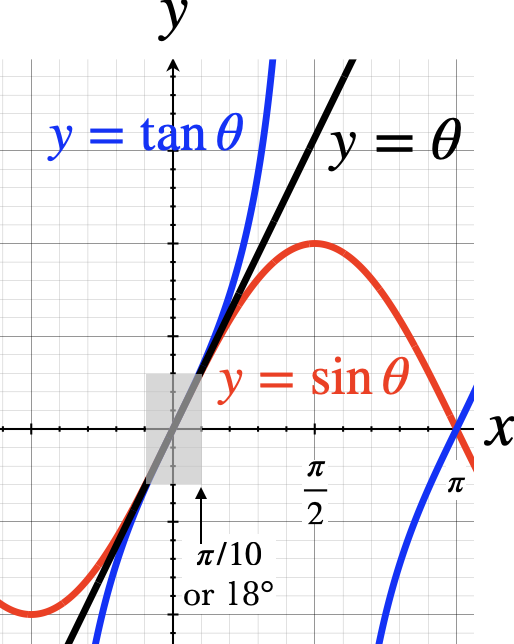
When the angle $\theta$ is small, then the sine of the angle and the tangent of the angle are approximately equal to each other, AND are approximately equal to $\theta$ in radians. This approximation is pretty darn good up to about $\pi/20$ or 9°, where $${\pi\over 10}=0.314,\qquad \sin{\pi\over 10}=0.309,\qquad \tan{\pi\over10}=0.325$$ which are all within 5\% of each other.