\(\def \u#1{\,\mathrm{#1}}\) \(\def \abs#1{\left|#1\right|}\) \(\def \ast{*}\) \(\def \deg{^{\circ}}\) \(\def \tau{\uptau}\) \(\def \ten#1{\times 10^{#1}}\) \(\def \redcancel#1{{\color{red}\cancel{#1}}}\) \(\def \BLUE#1{{\color{blue} #1}}\) \(\def \RED#1{{\color{red} #1}}\) \(\def \PURPLE#1{{\color{purple} #1}}\) \(\def \th#1,#2{#1,\!#2}\) \(\def \lshift#1#2{\underset{\Leftarrow\atop{#2}}#1}}\) \(\def \rshift#1#2{\underset{\Rightarrow\atop{#2}}#1}}\) \(\def \dotspot{{\color{lightgray}{\circ}}}\) \(\def \ccw{\circlearrowleft}\) \(\def \cw{\circlearrowright}\)
Appendix A: Miscellany
12.

Angle Measurements

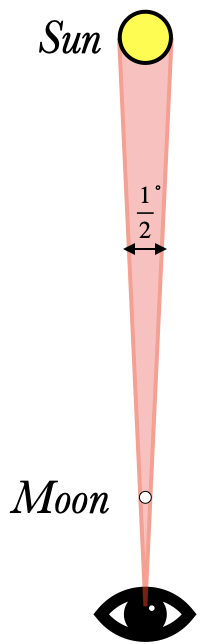
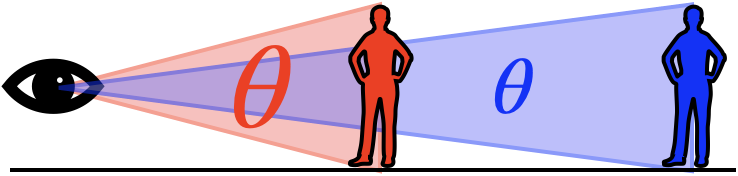
The moon is huge, and the Sun even bigger still, yet they appear to have the same "size" in the sky. When you walk towards a friend, they appear to get "bigger". This apparent size can't be something measured in meters. In fact, it makes sense to think of it as an angle, measured in degrees or radians. The larger this angle is, the larger the object appears to be in our field of vision. We can use this idea to even talk about things that don't really have a real "size", such as the apparent distance of $90\deg$ from the horizon to the zenith (the point straight above our heads).

If you hold out your hand at arm's length, you can use it to estimate the apparent size of objects.

If the apparent distance $\theta$ between two objects (or the width of an object) is relatively small, and if the two objects are roughly the same distance $D$ from the observer, then the actual distance $w$ between the objects can be approximated as an arc length: $$w = D\theta\qquad\hbox{($\theta$ measured in radians)}$$ So for instance, since the Sun is 150 million kilometers away, and its apparent size is about $0.5^\circ = 0.0087\u{rad}$, its actual width is roughly $w=(0.0087)(150\ten6\u{km})=$ 1.3 million kilometers across.