Torque and Equilibrium
We said that for a system to remain in static equilibrium, the horizontal forces must balance— the total force pointing left must equal the total force pointing right— and the same must be true for the vertical forces. Now we must add a third condition for equilibrium: that the torques on the object must balance as well. This means that the total clockwise and the counterclockwise torques on an object must be equal.Example
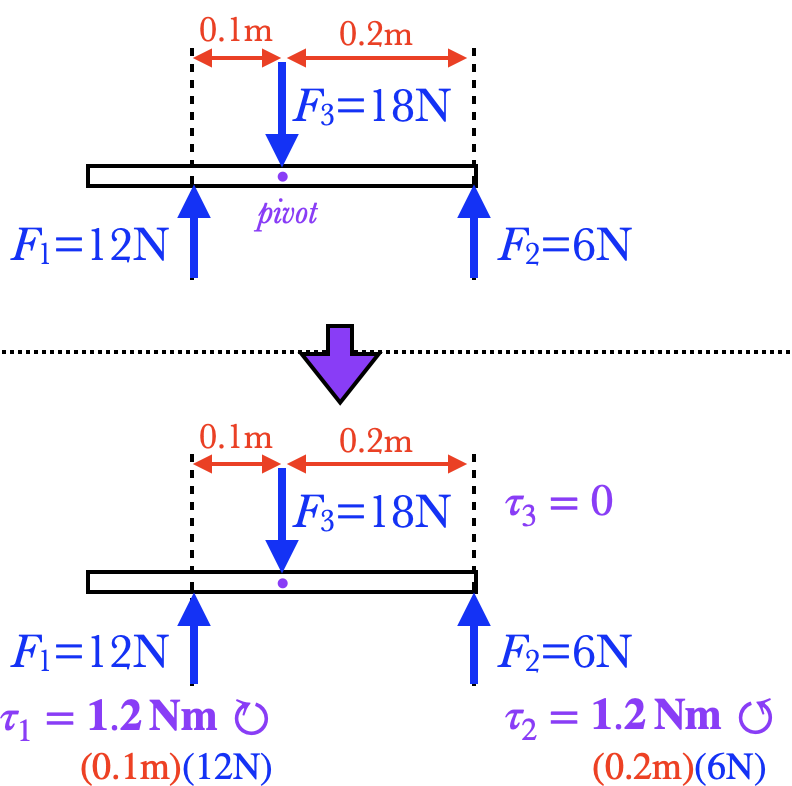
The figure shows a bar sitting on a table, as seen from above (so we can ignore gravity). It is pivoted in the center, and three forces are acting on the rod:
- A 12N upward force applied 0.1m to the left of the pivot. This creates a torque of $\tau=rF=(0.1\u{m})(12\u{N})=1.2\u{Nm}\cw$ on the rod.
- A 6N upward force applied 0.2m to the right of the pivot. This creates a torque of $\tau=rF=(0.2\u{m})(6\u{N})=1.2\u{Nm}\ccw$ on the rod.
- A 18N downward force applied at the pivot. The lever arm of this force is $r=0\u{m}$, so it doesn't exert a torque at all. (This force is probably being supplied by the pivot itself.)
Is the rod in equilibrium?
- The total upward force on the rod is 6+12=18N, and the downward force is also 18N, so the forces balance.
- The clockwise torque on the rod is $\tau_1=1.2$Nm, and the counterclockwise torque on the rod is $\tau_2=1.2$Nm, so the torques balance as well.
Therefore the rod is in equilibrium.
When an object is spinning around a particular point, like a wheel around an axle, then it's obvious where to put the pivot. But if an object is not spinning, then it's not spinning around any point. In this case, the "pivot" isn't a physical object so much as a mathematical choice: we can place our "pivot" anywhere we want, and so long as the torques balance around that pivot, they will balance around any pivot.
Example
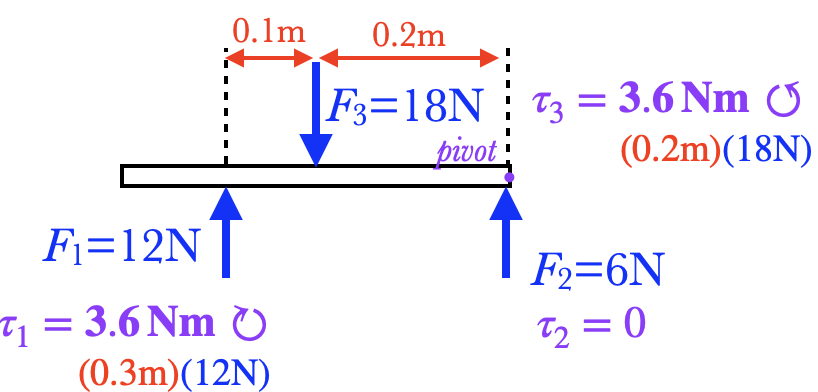
Consider the same rod, but now we'll move the "pivot" to the right end of the rod.
- The 12N force is now 0.3m away from the pivot. It still exerts a clockwise torque, but now its magnitude is $\tau=(0.3\u{m})(12\u{N})=3.6\u{Nm}$
- The 6N force now points directly at the pivot, so it exerts zero torque.
- The 18N force now exerts a counterclockwise torque around the pivot with $\tau=(0.2\u{m})(18\u{N})=3.6\u{Nm}$.
The individual torques are different, but the net result is the same: the torques balance, and the rod is still in equilibrium. You might want to try this same calculation with the pivot under $F_1$; you should get the same result.
Sometimes a clever choice of pivot can make a problem easier to solve, or allow you to see the problem in a different way.
Example
Consider a ruler with three forces on it: two pointing down on the left (purple) and at the center (red), and one pointing up on the right (blue). Is this rod in equilibrium?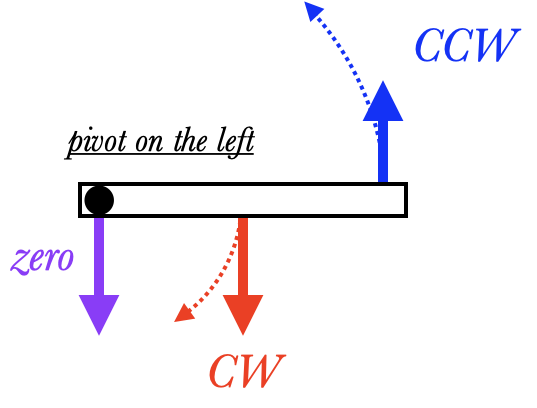
If the pivot is on the left, the blue force exerts a counterclockwise ($\ccw$) torque around that pivot while the red force exerts a clockwise ($\cw$) torque. The purple force exerts no torque because it is pointing directly away from the pivot. So it seems possible that this is in equilibrium, although we can't tell without numbers. Or can we?
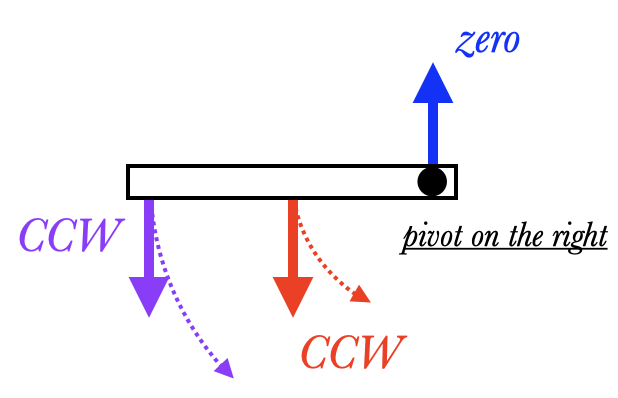
If we move the pivot to the right, then the blue force exerts zero torque, but the red and purple forces both exert counterclockwise torque. There is no way the torques can balance in this picture, and so the ruler cannot be in static equilibrium in either picture.
In equilibrium problems, you can place the pivot anywhere you want, and the result will be the same. (This would not be true if the object starts to spin, however.)
Use this demo to practice calculating torques and finding equilibrium. Remember that you should measure all distances from the pivot, but you can put the pivot anywhere you like. (I recommend pencil and paper unless you're good at mental arithmetic.)