\(\def \u#1{\,\mathrm{#1}}\) \(\def \abs#1{\left|#1\right|}\) \(\def \ast{*}\) \(\def \deg{^{\circ}}\) \(\def \redcancel#1{{\color{red}\cancel{#1}}}\) \(\def \BLUE#1{{\color{blue} #1}}\) \(\def \RED#1{{\color{red} #1}}\) \(\def \PURPLE#1{{\color{purple} #1}}\) \(\def \th#1,#2{#1,\!#2}\) \(\def \lshift#1#2{\underset{\Leftarrow\atop{#2}}#1}}\) \(\def \rshift#1#2{\underset{\Rightarrow\atop{#2}}#1}}\) \(\def \dotspot{{\color{lightgray}{\circ}}}\)

Standing Waves

Standing waves on a string have a number of relevant variables: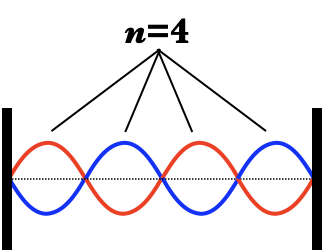

• The length $L$ of the standing wave is the distance between the ends.
• The speed $v$ is the speed a wave would have if it travelled along the string.
• The mode $n$ of the standing wave is the number of antinodes: that is, the number of crests or troughs.
• The frequency $f_n$ of the nth mode is the frequency of the antinodes as they move up and down.
• The wavelength $\lambda_n$ is the distance between two crests, two troughs, etc. It is related to the length as $$\lambda_n={2L\over n}$$
• The fundamental frequency $f_1$ is the lowest frequency that can exist on this string. It is given by $$f_1={v\over 2L}$$, and it is related to the frequency of the $n$th mode by $$f_n=nf_1$$

I suggest you start by listing these six variables, fill in what is given, and then find the appropriate equations to find the variable you want.