\(\def \u#1{\,\mathrm{#1}}\) \(\def \abs#1{\left|#1\right|}\) \(\def \ast{*}\) \(\def \deg{^{\circ}}\) \(\def \redcancel#1{{\color{red}\cancel{#1}}}\) \(\def \BLUE#1{{\color{blue} #1}}\) \(\def \RED#1{{\color{red} #1}}\) \(\def \PURPLE#1{{\color{purple} #1}}\) \(\def \th#1,#2{#1,\!#2}\) \(\def \lshift#1#2{\underset{\Leftarrow\atop{#2}}#1}}\) \(\def \rshift#1#2{\underset{\Rightarrow\atop{#2}}#1}}\) \(\def \dotspot{{\color{lightgray}{\circ}}}\)

Doppler Effect

If a sound source has an initial frequency is $f_{src}$, and the source or an observer is moving, then the frequency $f_{obs}$ is heard by the observer is $$f_{obs}=f_{src}{\color{blue}v_w\mp v_{obs}\over \color{red}v_w\pm v_{src}}$$

$v_w$ is the speed of the sound wave. Under normal conditions, $v_w=343\u{m/s}$ in 20°C air. Start by writing $v_w$ in the numerator and denominator.

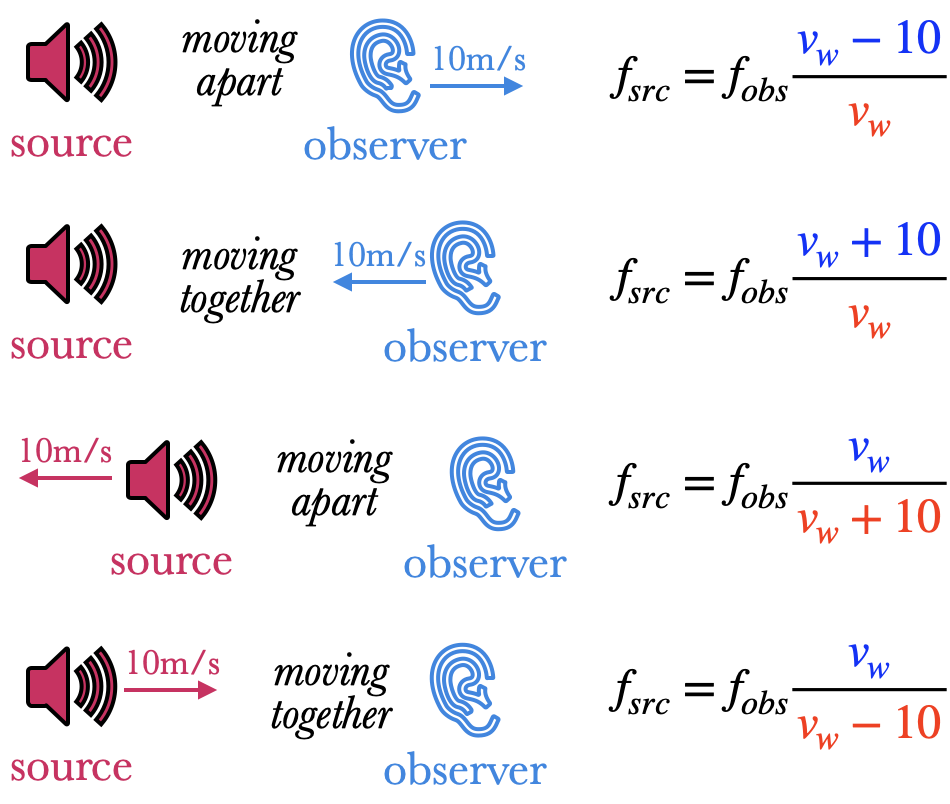
• If the observer is moving away from the source, then subtract the observer's speed in the numerator.
• If the observer is moving towards the source, add the speed to the numerator.
• If the source is moving away from the source, then add the source's speed to the denominator.
• If the source is moving towards the source, subtract the speed from the denominator.
• It's possible that both source and observer are moving, in which case you will have terms in both numerator and denominator.

The end result should be smaller than $f_{src}$ if the two are moving away from each other, and should be larger if they are moving towards each other.