Electric Current

The steady motion of charge in a single direction is called current $I$. It is equal to the amount of charge that flows through a conductor (or by a specific point in the conductor) per second, and is measured in amperes (A).

An ampere is a large but not overly large current, which means there might be a coulomb of charge flowing through the wires in your wall every second or maybe every minute. We mentioned earlier that a coulomb is a huge charge, but that is only when we have a coulomb of excess charge in one place. Wires are generally neutral, which means that they contain equal numbers of protons and electrons. As the electrons flow, each electron replaces the electron in front of it, and so the wire remains neutral so long as the electrons continually have a place to move. If there is a break in the wire, however, then charge will build up at that spot, and the charge buildup will bring the incoming current to a halt.

A similar thing would occur if more current flows into an object than out of it. If more current flows into an object than out, then charge will build up inside the object (it can't disappear, after all). This buildup of charge will decrease the current coming in, and increase the current going out, until eventually the current becomes constant again. This is an important rule when studying circuits:

If moving charges are a bit too abstract for you, you might imagine current as flowing water (see Flow Rate) or as cars moving on a highway. If more cars enter onto a bridge than exit it, for instance, then that's the sign of a traffic jam, or a non-steady flow of cars. It is possible for current to split up or merge together, the way traffic can do so, so long as the total current in equals the total current out.

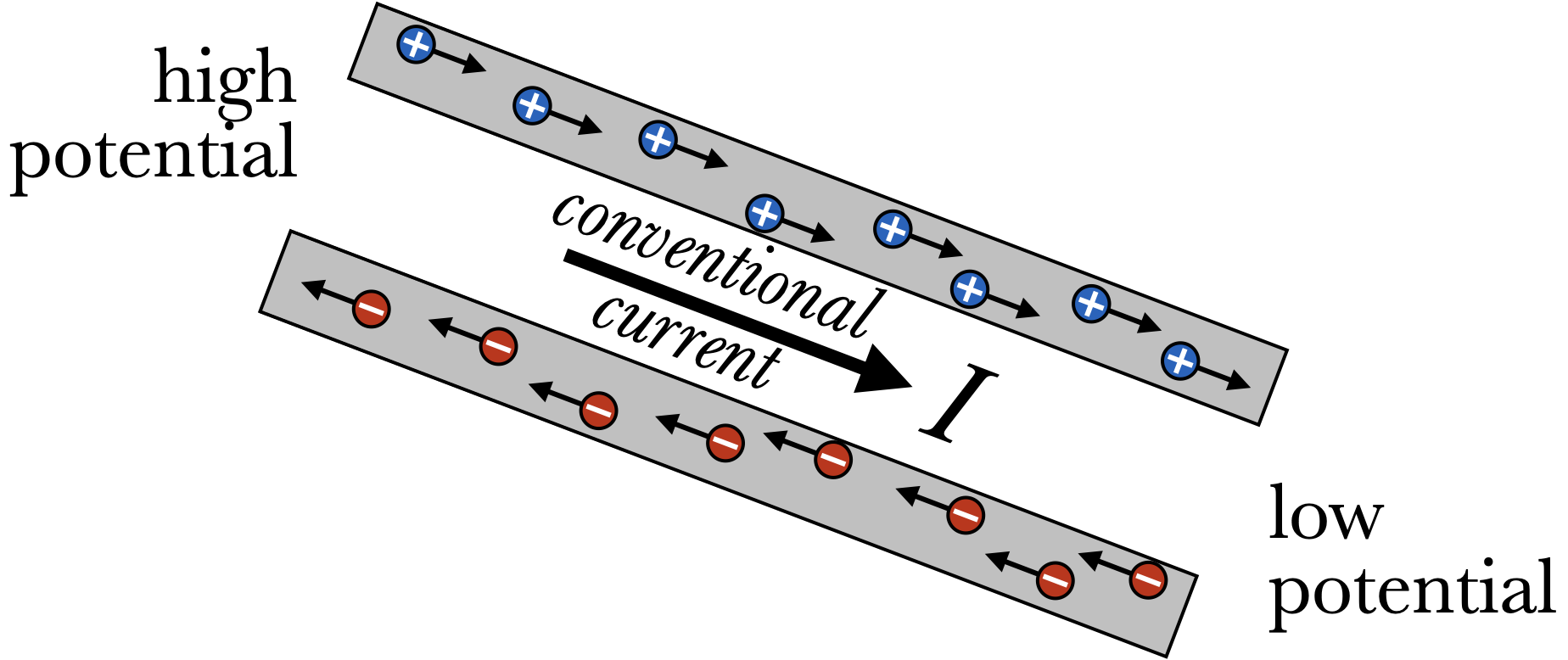
Currents have direction, but they are not exactly vectors: angles don't matter, for instance. What does matter is whether the current is flowing in or out, left or right, etc. Since metal is the most common conductor and electrons are the charge carriers inside, we might set the direction of the current equal to the direction the electrons move. That is inconvenient, however, primarily due to the negative charge of the electron (thanks, Franklin!) Fortunately, a flow of negative charge in one direction is mostly equivalent to a flow of positive charge in the other direction, and so we define a conventional current which points in the direction that positive charge carriers would move in the same situation. That means that current tends to move from higher to lower potential, which fits nicely with our metaphor of water flowing downhill. Therefore