Potential of Conductors

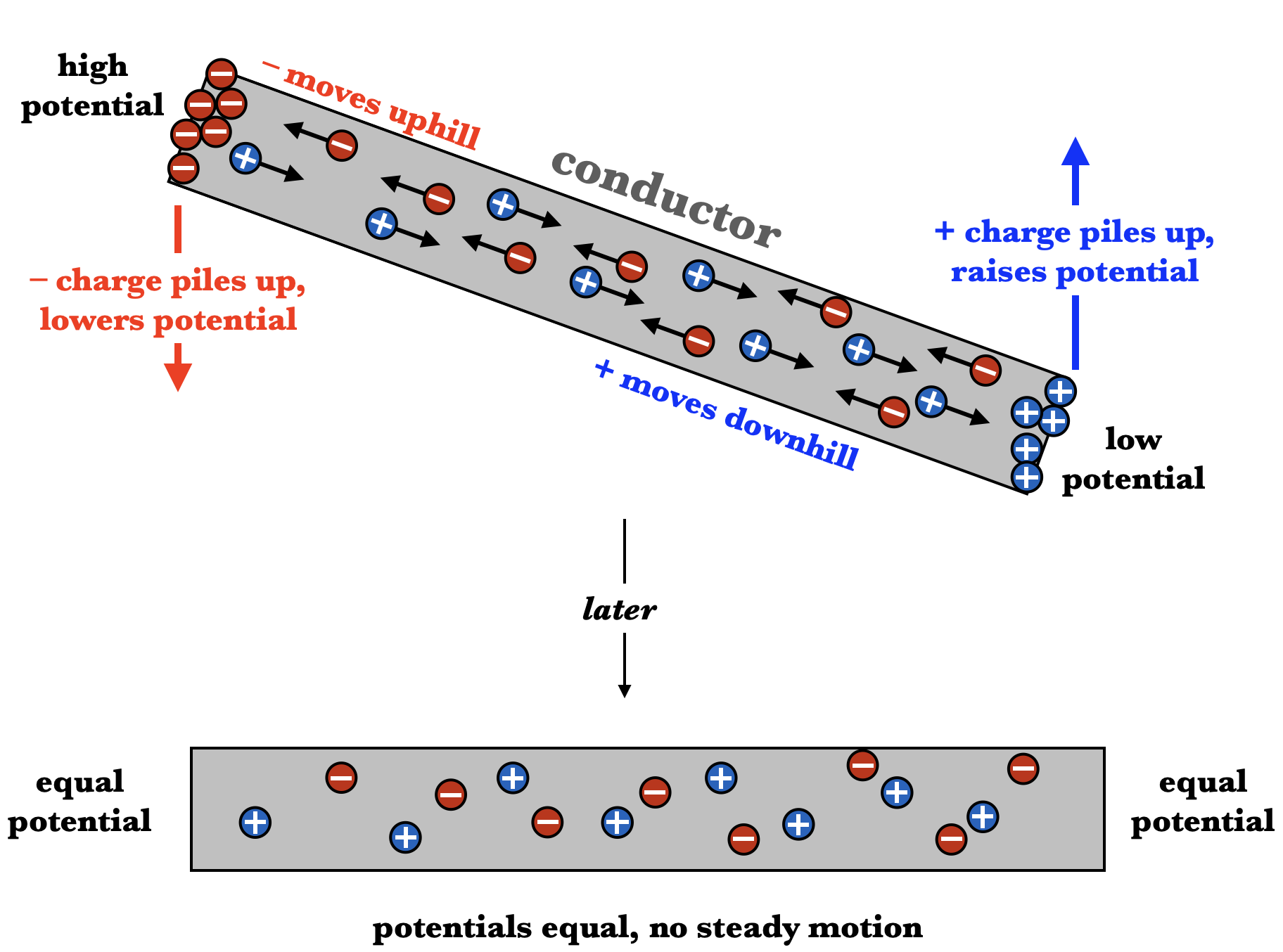
Suppose one end of a conductor has a higher potential than the other. Because conductors have Charge Carriers, the free positive charges will tend to rush downhill, while the free negative charges will tend to rush uphill. But charges can change potential, not just react to it, so as the positive charges pile up on the lower end, they cause that potential to rise, while the negative charges cause the upper end to drop in potential, until the two potentials are equal to each other.

This process takes milliseconds, and so in most cases the electric potential inside a conductor is the same everywhere inside that conductor. Different conductors might have different potentials, however.

This means that the surface of a conductor is an equipotential surface, no matter what its shape. Outside the conductor, the equipotential lines initially follow the contours of the conductor's surface, until eventually smoothing out. If the conductor has a net charge, then eventually the equipotential surfaces form circles centered on the conductor.