Pipes

You can create standing waves in columns of air too, such as a flute, clarinet, organ pipe, or even a jug. The standing waves that can be created depends on whether the ends of the pipe are open or closed. If the end of the pipe is "open", then the column of air inside is in contact with the atmosphere, and so its pressure is fixed at $P_{atm}$; in other words, we have a node at the open end. If the end of the pipe is closed, on the other hand, then the pressure can vary, and in fact an antinode will form at the closed end.

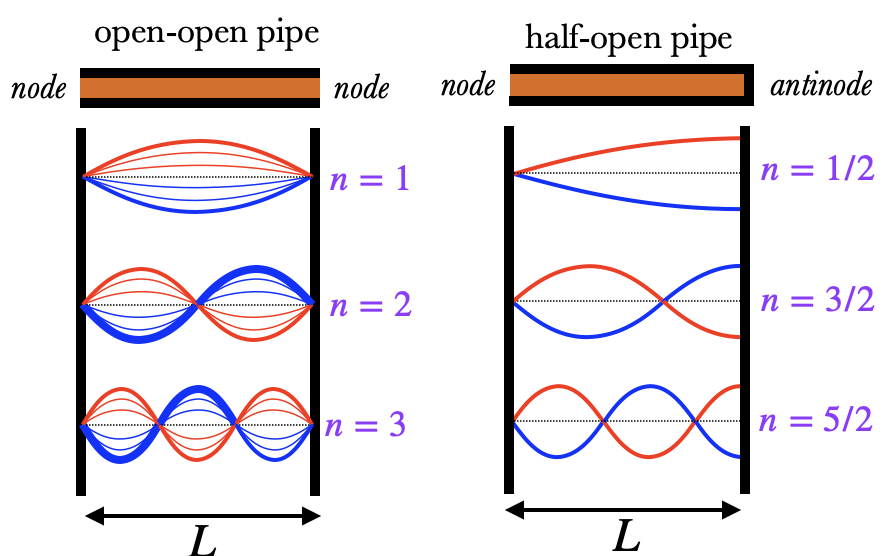
The figures here show the smallest possible standing waves following these conditions. (Remember that the lines here are actually graphs of the pressure across the pipe.) For a pipe that is open on both ends, we need a node at both ends, and so the standing waves are the same as those we saw in Standing Waves. For a half-open pipe, on the other hand, the standing waves are different, requiring an antinode on the closed side. The first mode has half an antinode, ($n=\frac12$), the second mode is one-and-a-half antinodes ($n=\frac32$), the third mode is two-and-a-half antinodes ($n=\frac52$), and so forth.

The frequency of both pipes obeys the same formula as before: $f_n=n{v\over 2L}$. However, because the half-open pipe starts with $n=1/2$, its fundamental frequency is $f_{1/2}={v\over 4L}$, which is half the fundamental frequency of the open-open pipe. This is why a clarinet sounds lower than a flute, even though they are roughly the same length. The frequencies of a half-open pipe's overtones are $f_{p/2}=pf_{1/2}$, where $p=1,3,5,\dots$.