Interference
When two wave pulses or waves overlap in a medium, they don't interact with each other per se: if two travel through the same space they just pass through each other. (Imagine how strange it would be otherwise, if flashlight beams or sound waves bounced off each other!) However, in the area of the medium where two (or more) pulses exist, the medium feels the effect of both pulses at once, a phenomenon called superposition.
It might be easiest to understand this if we think of a wave pulse as a set of instructions to the medium. A crest tells the medium "go up!" A trough tells the medium "go down!" If two crests overlap each other, the instructions reinforce each other, and the medium rises higher than either of the two crests by themselves. This is called constructive interference. On the other hand, if a crest and a trough overlap, then the two instructions cancel each other out ("go up! now go back down!") and you end up with destructive interference.
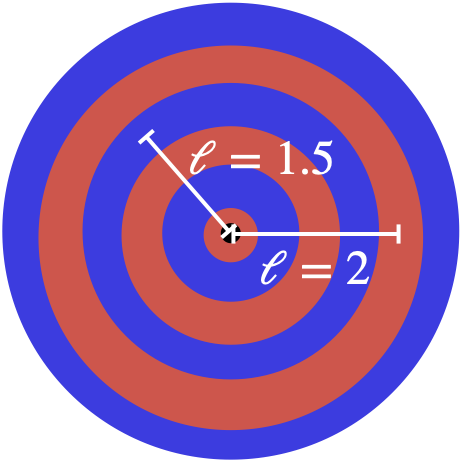
In the case of a sinusoidal wave with wavelength $\lambda$ which is created by a source, we will define the path length $\ell$ at any location as
where $L$ is the distance from the source to the location in question. In other words, the path length is the number of cycles the wave must go through in order to reach that spot.

If we have two sources of waves with the same wavelength, and the sources are in phase with each other (that is, produce crests and troughs at the same time), then the two waves interfere constructively at any given location if the difference in their path lengths is close to an integer. They interfere destructively, on the other hand, if the difference in their path lengths is close to an integer plus one-half. In short,
If $\Delta\ell$ is an integer plus 0.5, we have destructive interference.
Here's an interactive animation where you can see this at work.