Inclined Plane
One popular problem in physics is to study a box sitting on or sliding down an inclined plane. There are usually at least three forces acting on the box: its weight, the normal force from the plane, and some sort of frictional force pointing up the hill.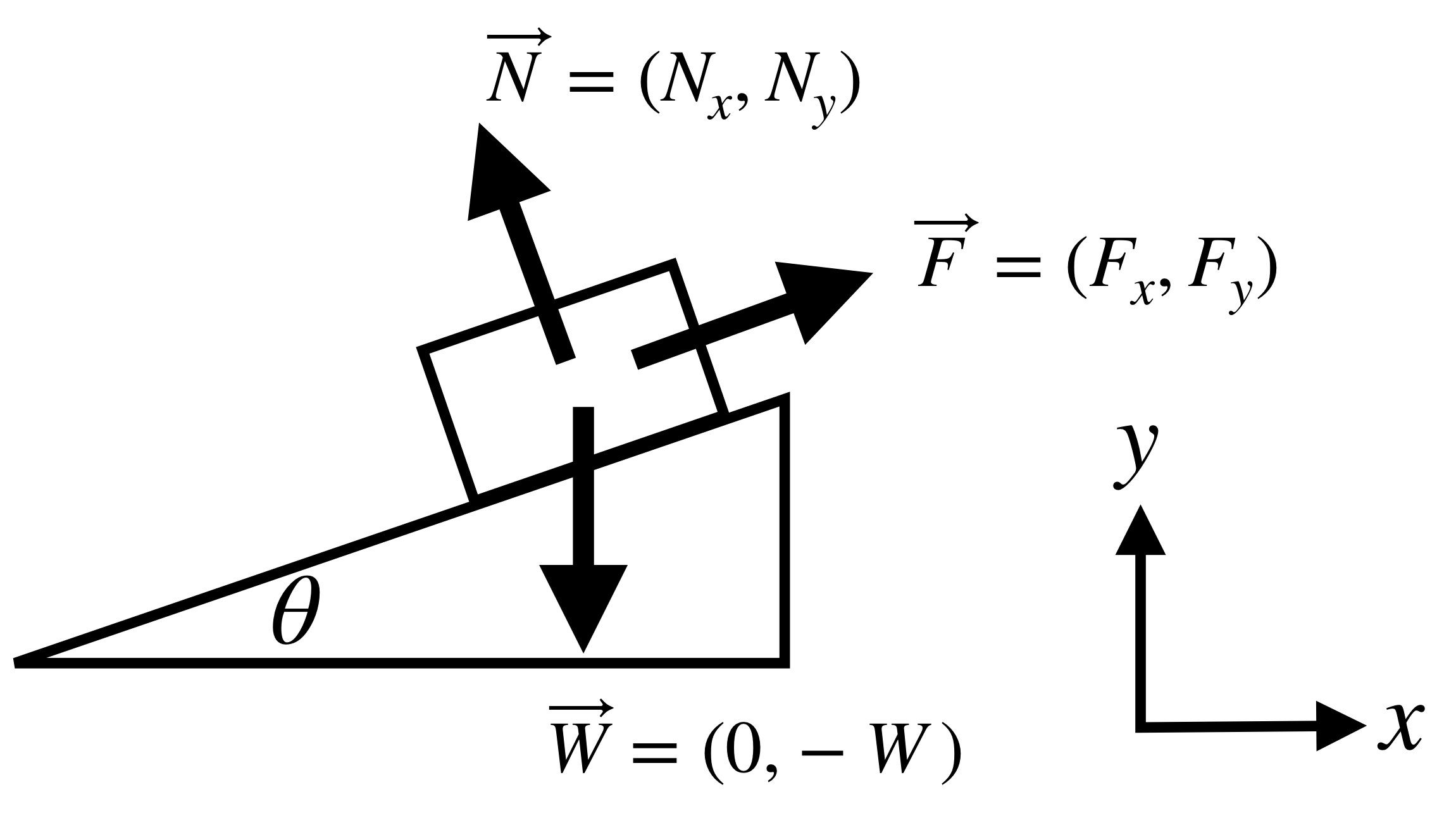
If we use the ordinary axis with x pointing to the right, then we need to break the frictional force and the normal force down into its components. This is a bit of a nuisance. However, nobody said we needed to use this particular basis.
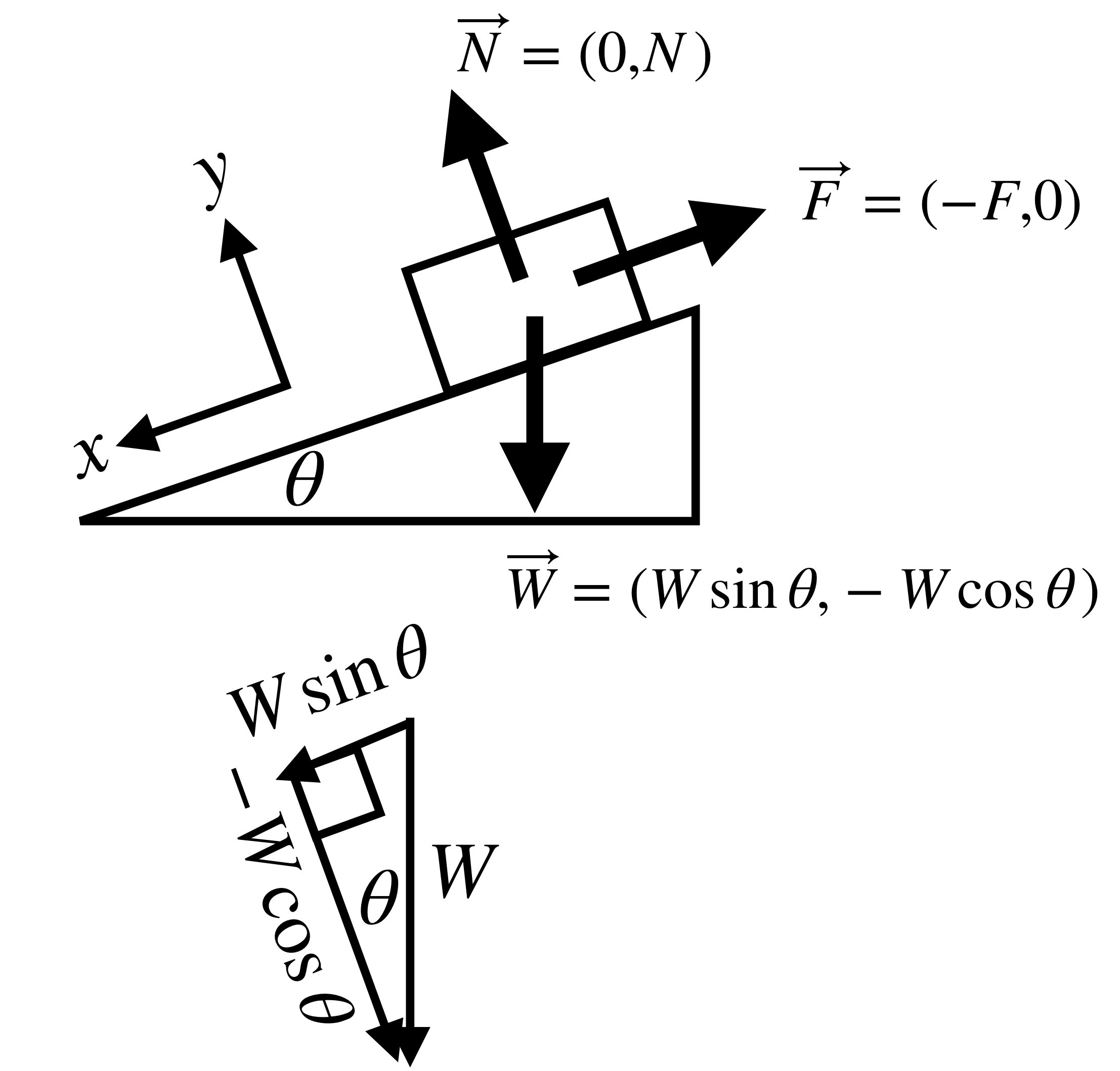
Notice that the normal force and the frictional force are perpendicular to each other, so we can use tilted coordinate axes instead, that point down along the hill and straight away from the hill's surface, as shown in the second figure. Now the normal force and the frictional force can be written simply. Unfortunately now the weight has to be written in component form. This can be hard to figure out on the fly, so feel free to refer back to this diagram when working on inclined plane problems, and write $$\begin{align} N&=(0,+N)\\ W&=(W\sin\theta,-W\cos\theta)\\ F&=(\pm F,0) \quad \text{sign depends on direction}\\ \end{align}$$