Vector Basis and Notation

Adding vectors graphically can be fun, but it would be frustrating to get precise answers out of it. Sometimes we need numbers.

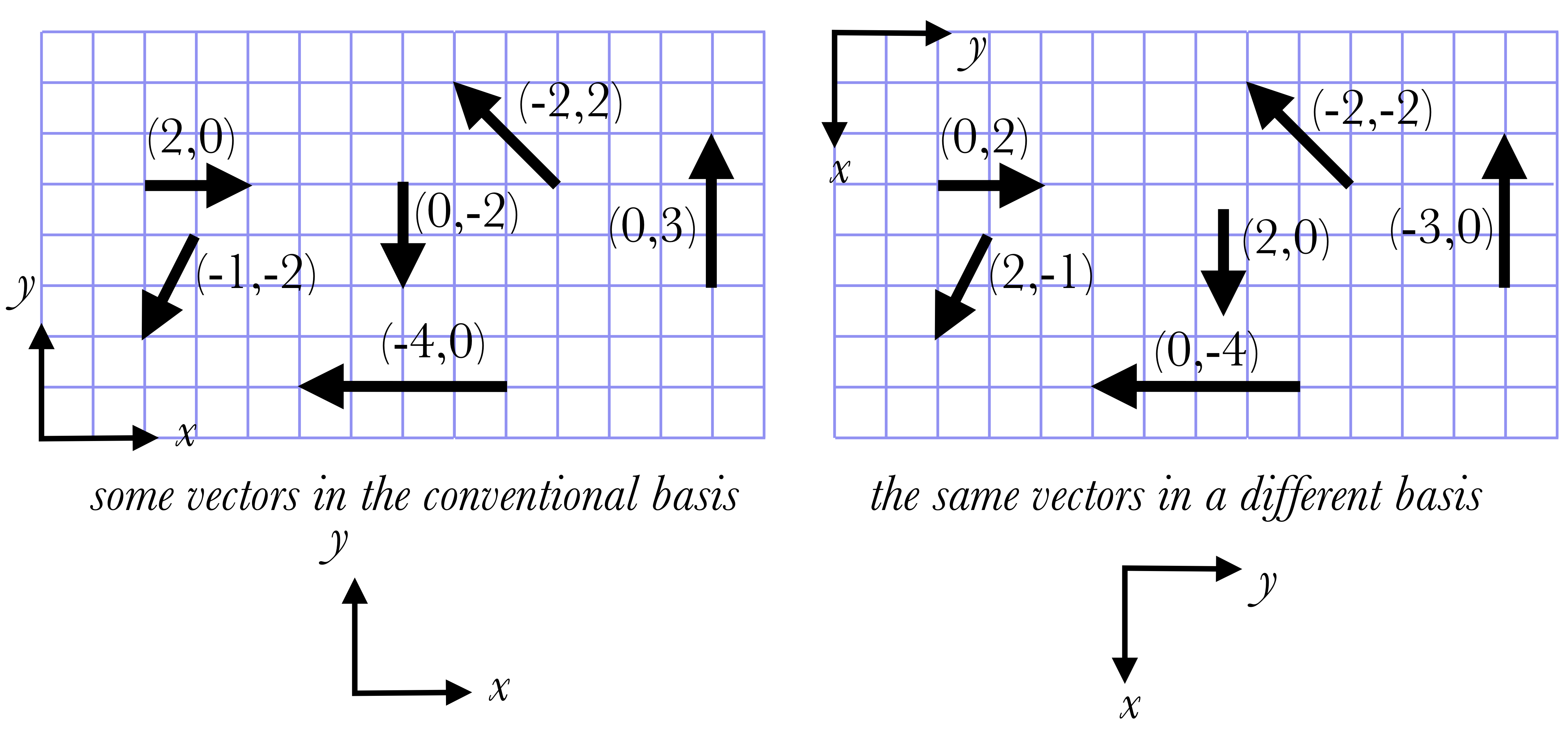
Before we can write a vector this way we must specify a basis: that is, we need to define a positive x-direction, and a positive y-direction perpendicular to it. (If we're working in 3D we will need a "z" as well.) The conventional basis is the one shown here: with $x$ pointing to the right and $y$ pointing up, but you should not assume that this is always the case.

We can write vectors as a set of two or three numbers, called a tuple, like this force: $\vec F = (4, − 5)\u{N}$. The individual numbers 4 and –5 are called components of the vector, and are written $F_x=4$ and $F_y=-5$. The picture on the right shows the vector (4,–5) given the conventional basis above: the vector goes “over 4 and down 5”.

There is nothing particularly special about the conventional basis; we can use whatever basis we want.. For instance, we could make x point down and y point to the right. In that case, the same vector would be written (5,4).

Demo

Footnote

Instead of using tuple notation, physicists will often write vectors using unit-vector notation, which looks like this: $$\vec F=(F_x,F_y,F_z) = F_x\,\hat i + F_y\,\hat j + F_z\,\hat k \quad\text{ or }\quad F_x\,\hat x+F_y\,\hat y+F_z\,\hat z$$ So for example, they would write $(3,-5)$ as $3\hat i-5\hat j$ or $3\hat x-5\hat y$.

The symbols with the hats, like $\hat x$, are called unit vectors. The unit vectors $\hat i$ and $\hat x$ are vectors that point in the positive-$x$ direction, which have a length of 1. (Not 1 meter or 1m/s or anything, just "1".) Thus $3\hat x$ is a vector which also points in the positive $x$ direction, but which has a length of $3$.

We won't use this notation in this book, but you may see it elsewhere.