\(\def \u#1{\,\mathrm{#1}}\) \(\def \abs#1{\left|#1\right|}\) \(\def \ast{*}\) \(\def \deg{^{\circ}}\) \(\def \tau{\uptau}\) \(\def \ten#1{\times 10^{#1}}\) \(\def \redcancel#1{{\color{red}\cancel{#1}}}\) \(\def \BLUE#1{{\color{blue} #1}}\) \(\def \RED#1{{\color{red} #1}}\) \(\def \PURPLE#1{{\color{purple} #1}}\) \(\def \th#1,#2{#1,\!#2}\) \(\def \lshift#1#2{\underset{\Leftarrow\atop{#2}}#1}}\) \(\def \rshift#1#2{\underset{\Rightarrow\atop{#2}}#1}}\) \(\def \dotspot{{\color{lightgray}{\circ}}}\) \(\def \ccw{\circlearrowleft}\) \(\def \cw{\circlearrowright}\)
Chapter 7: Thermodynamics
8.

Carnot Engines

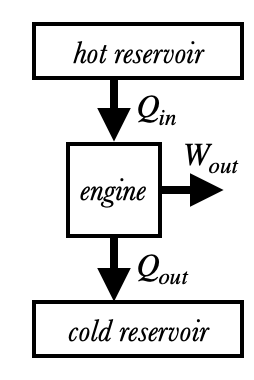
(no alternate text)

As we discussed in Perpetual Motion, it is impossible for a heat engine to convert all heat $Q_{in}$ into work $W_{out}$ due to the Second Law of Thermodynamics: in other words, a heat engine can never have 100% efficiency. Instead, the efficiency always obeys the bound

$$\eta\le {T_H-T_C\over T_H}$$

where $T_H$ and $T_C$ are the temperatures (in Kelvin!) of the hot and cold reservoirs, respectively.

Example

For instance, a heat engine which operates between steam (373K) and room temperature (293K) cannot have an efficiency above $${T_H-T_C\over T_H}={373-293\over 373}=21\%$$
We can increase the maximum efficiency of an engine by increasing the difference $T_H-T_C$ between the two reservoirs: by using a hotter hot reservoir, say, or a colder cold reservoir.

A Carnot engine is a heat engine which is able to operate at the maximum efficiency allowed for a given set of temperatures. It works by using some sort of gas such as air, and repeats the following four steps:

  1. Quickly raise the gas's temperature so that it is almost equal to $T_H$, without letting any heat flow. This can be done by compressing the gas quickly, for example. (If you've ever used a manual air pump you might have noticed that constantly compressing the air inside causes the pump to warm up.)
  2. Allow heat $Q_{in}$ to flow from the hot reservoir into the gas. This is why the gas needs to be slightly cooler than the reservoir, or else heat won't flow at all.
  3. Quickly lower the gas's temperature so that it is almost equal to $T_C$, without letting heat flow. This is the step where work $W_{out}$ flows out of the gas into the environment. For example, the gas may push outward on a piston, and as it expands, the gas cools down.
  4. Let heat $Q_{out}$ flow from the engine into the cold reservoir.
  5. Repeat.

Carnot engines are not typically used in practice, not because they are impossible to build, but because they are very slow. The rate at which heat flows from one object to another depends partly on the temperature difference between them: heat flows faster out of your hand into snow, than it does from a room temperature object. In steps 2 and 4, the gas and the reservoir are very close in temperature to each other, and so it takes heat a very long time to flow, and thus the power of the heat flow is small. Therefore Carnot engines are high-efficiency but low-power (a tradeoff you may be familiar with from different types of car).