Object Underwater
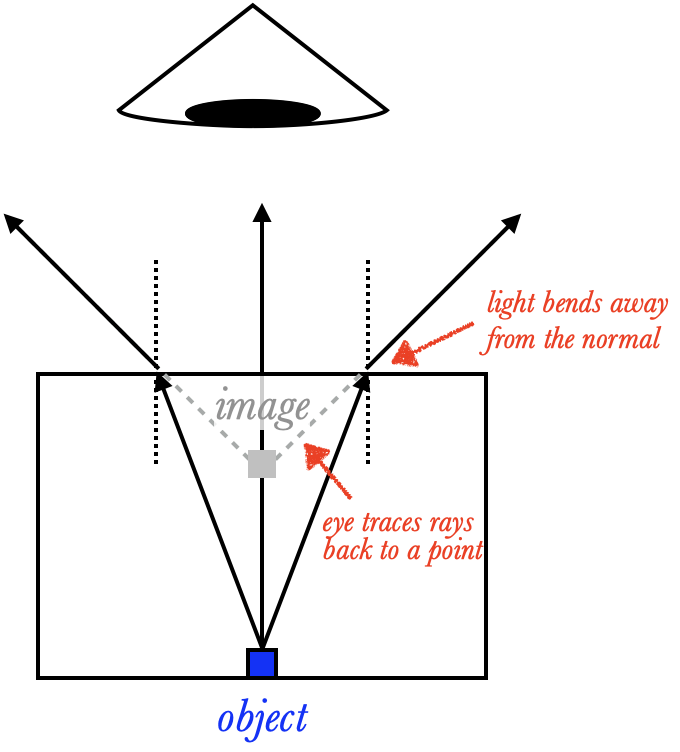
It's not just mirrors that create images. For example, consider an object sitting on the bottom of a pool. Rays of light are emitted from the object and continue in straight lines until they reach the surface of the water: at that point, the rays refract away from the normal. Our eyes, seeing these bent rays, trace them back to a point higher in the water than the original object, and thus see an image there. This is why swimming pools look shallower than they are. We can approximate the depth of the image as $$d_i\approx {n_t\over n_i}d_o$$ where $n_i$ is the index of refraction of water, and $n_t$ is the index of refraction of air. (Though of course this works with other combinations of materials as well.) In the case of water and air, $n_i={4\over3}$ and $n_t=1$, so $d_i\approx {3\over4}d_o$, so the pool appears 25\% shallower than it really is.
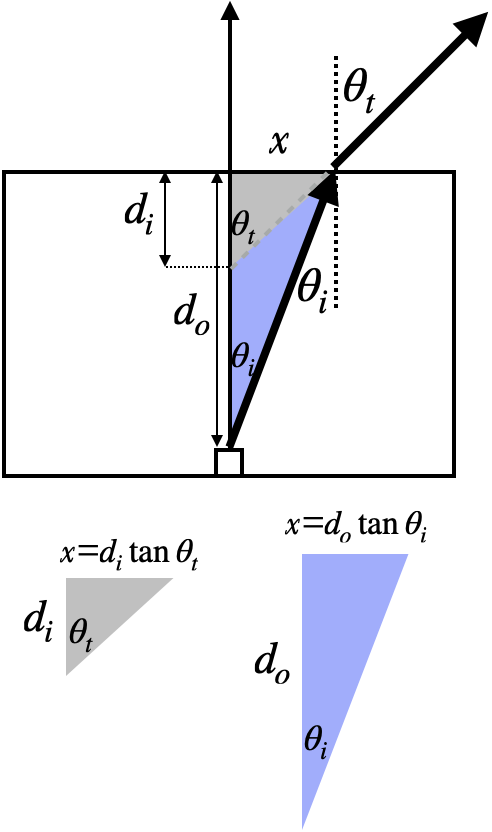
Proof
We can use some geometry and trigonometry to find how deep the object is. We let $\theta_i$ and $\theta_t$ be the incident and transmitted angles of the bold ray. Snell's Law says that $$n_i\sin\theta_i = n_t\sin\theta_t \implies {\sin\theta_i\over\sin\theta_t} = {n_t\over n_i}$$ We highlight two right triangles, grey and blue, and using the normal and the other ray as parallel lines, we see that the grey triangle has an angle $\theta_t$ and the blue triangle has an angle $\theta_i$, both opposite the horizontal line at the top which both triangles share, which we'll call $x$.
Now the tangent of an angle in a triangle is the length of the opposite side ($x$, in this case), divided by the adjacent side, so we can write $x$ as $$x=d_i\tan\theta_t \quad \hbox{AND} \quad x=d_o\tan\theta_i$$ Since these have to be equal, $$d_i\tan\theta_t = d_o\tan\theta_i \implies d_i=d_o{\tan\theta_i\over\tan\theta_t}$$ However, for small angles, the sine of the angle is roughly equal to the tangent of the angle (see Trigonometric Functions). Thus $$d_i=d_o{\tan\theta_i\over\tan\theta_t} \approx d_o{\sin\theta_i\over\sin\theta_t}$$ Using the result from Snell's Law above, we see that $$d_i\approx {n_t\over n_i}d_o$$