\(\def \u#1{\,\mathrm{#1}}\) \(\def \abs#1{\left|#1\right|}\) \(\def \ast{*}\) \(\def \deg{^{\circ}}\) \(\def \tau{\uptau}\) \(\def \ten#1{\times 10^{#1}}\) \(\def \redcancel#1{{\color{red}\cancel{#1}}}\) \(\def \BLUE#1{{\color{blue} #1}}\) \(\def \RED#1{{\color{red} #1}}\) \(\def \PURPLE#1{{\color{purple} #1}}\) \(\def \th#1,#2{#1,\!#2}\) \(\def \lshift#1#2{\underset{\Leftarrow\atop{#2}}#1}}\) \(\def \rshift#1#2{\underset{\Rightarrow\atop{#2}}#1}}\) \(\def \dotspot{{\color{lightgray}{\circ}}}\) \(\def \ccw{\circlearrowleft}\) \(\def \cw{\circlearrowright}\)
Chapter 2: Laws of Motion
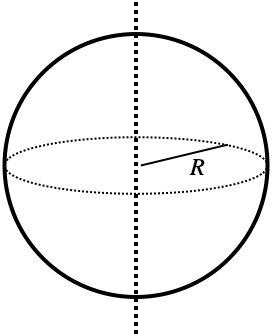
10.

Moment of Inertia

When an unbalanced torque is applied to an object, it will either cause that object to spin or else change the rate at which it spins. This change is called the angular acceleration $\alpha$ of the object. We will talk about this in more detail in Angular Acceleration, but it works much the same way as acceleration does. For instance, an angular acceleration applied in the same direction as an object's spin will make it spin faster, while an angular acceleration applied in the opposite direction will slow it down.

Angular acceleration and net torque are related by a rule quite similar to Newton's Second Law :

$$\alpha={\tau_{net}\over I}$$

Moment of Inertia
\(I\)
N m2
The letter $I$ represents the object's moment of inertia, which is a measure of how difficult it is to change the object's rate of spin. For instance, it is much harder to stop a heavy stone wheel from spinning than the wheel on a toy car, because the former has a larger moment of inertia. Moment of inertia is proportional to an object's mass, but it also depends on how that mass is distributed and the location of the axis: the farther away from the axis the mass is, the larger the moment of inertia.

Column

(no alternate text)

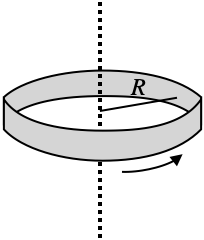
For an object where all the mass $M$ is the same distance $R$ from the axis, the moment of inertia is $$I_{ring}=MR^2$$. This is also true for a half-ring, a rock spinning around the axis—any scenario where all of the mass is the same distance from the axis.

Column

(no alternate text)

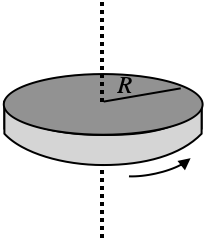
If the same mass $M$ is shaped into a disk of radius $R$, then most of the mass is much closer to the axis than it was in the ring, and so the moment of inertia is smaller. One can use calculus to show that $$I_{disk}=\frac12MR^2$$

Column

(no alternate text)

Similarly, a hollow sphere rotated around its axis has a moment of inertia of $$I_{sphere}=\frac23MR^2$$ but a solid sphere (called a ball) has a smaller moment of inertia for the same mass, $$I_{ball}=\frac25MR^2$$

Column

(no alternate text)

The moment of inertia depends on the location and orientation of the axis. For example, if you take the same ring we saw before but rotate it on end, then not all of the mass is the same distance from the axis, and so the moment of inertia is smaller: $\frac12MR^2$ instead of $MR^2$.

You can find an extensive list of moments of inertia on Wikipedia