Free Fall

An object is in free fall when the only force acting on it is gravity. Technically, this only occurs in a vacuum, because air resistance is always present. In practice, however, we can often ignore air resistance and still get a pretty good idea about how an object behaves, although the speeds we predict may be too high.

The net force on an object in free fall is ${\vec{F}}_{n e t} = m g ↓$ , so we know from Newton's Second Law that its acceleration is $\vec{a} = \frac{{\vec{F}}_{n e t}}{m} = \frac{m g ↓}{m} = g ↓$ where $g$ is our old friend $9.8 m / s^{2}$ .

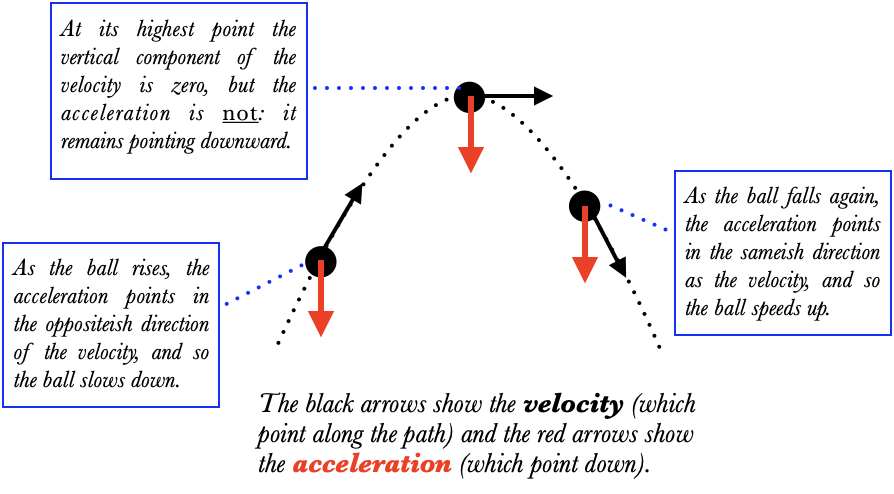
Although it is called free fall, the term applies to any object which is only experiencing the force of gravity—that is, any object not in contact with anything. When I throw a ball into the air, that ball is in free fall the entire time it is in the air: when it goes up, at the top of its flight, and when it comes back down: the acceleration of the ball is downward during its entire flight. This downward acceleration has a different effect at different points in the flight: