Diverging Devices

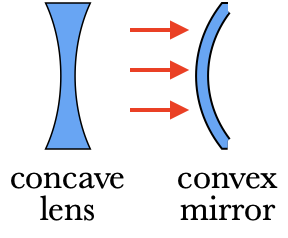
A diverging device is a lens or mirror which causes rays to diverge more (or perhaps make converging rays converge less). Concave lenses and convex mirrors are examples of diverging devices. Because diverging devices cannot bring diverging rays to a point, they only create virtual images.

They have focal points like converging devices too, but the definition is slightly different. When parallel horizontal rays strike a diverging device, the rays diverge so that they appear to come from the focal point. It's as if the focal points are swapped compared to converging devices, and so the focal length of diverging devices are considered to be negative: $f<0$.

The same lens equation works for diverging devices too, with a negative $f$. If we write $f=-\abs{f}$, the image distance becomes $$d_i=-{d_o\abs{f}\over d_o+\abs{f}}$$ The numerator and denominator are both positive, so the negative sign means $d_i<0$ always: the images are always virtual, as we said above. The magnification can be written $$M={\abs{f}\over d_o+\abs{f}}$$ This is always positive, and because the denominator is always larger than the numerator, the magnification is always less than 100%.

In short, diverging lenses and mirrors always create virtual images which are smaller than the original object. This might not seem very useful, but a smaller image means that more of the image can be fit into view, as with a door peephole or the curved mirrors one sometimes sees in the corners of stores.