18. (Problem Solving)

Drawing Force Diagrams

For each object of interest in the problem:

Red

1. Make a list of the forces acting on that object.

Start with weight (if applicable).
Identify all objects that touch the object.
Any pulling on the object (by a rope e.g.) is tension.
Any surface in contact may supply a normal force or a frictional force or both.
If the surfaces are sliding against each other, then it is kinetic friction. If not, then it is static friction.

Green

2. Draw a force diagram of the object with all the forces labelled, either with their value (if given) or with a distinct variable name. (Use subscripts if there are, for instance, more than one normal force.)

Weight points down.
Tensions point in the direction of the rope or pull
Normal forces always point towards the object, perpendicular to the surface of contact.
Kinetic frictional forces point along the surface, opposite the direction of motion.
Static frictional forces point along the surface, in whatever direction is necessary to maintain equilibrium. (If you cannot determine the direction, pick one at random.)

Purple

3. Define the positive x and y directions by drawing an axis.

Blue

4. Next to the list you wrote in Step 1, draw two columns, for x and y. Write the components of each force in the table next to the force's name:

If the force points along one of the axes, put a dash in the other column.
If the force does not point along one of the axes but at an angle, then you will need to break it down into its components: if the magnitude is X then one column will be “X cos(angle)” and the other will be “X sin(angle)”.
Write a $+$ or $-$ in front of each entry, indicating whether it points in the positive or negative direction. You may omit the sign if the force is a variable and you don't know the direction it points in.

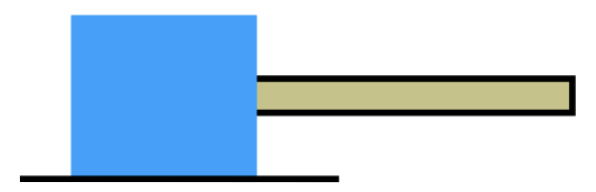
Example: A 8N block is being pulled by a rope but does not move.

Table

Step 1	Step 4
Force	x	y
Weight	—	$- 8$
Tension, rope	$+ T$	—
Normal, floor	—	$+ N$
Static friction, floor	$- S$	—

Nohead

Step 2

Nohead

Step 3