Wavespeed and The Wave Equation

How fast does a wave move? If we consider this series of snapshots of a wave, we can change that question to "how fast does that red dot move"? Since the distance between those two dashed lines is the wavelength $\lambda$, and the time it takes for the dot to move from the first to the second is the period $T$, then the speed of the wave is distance divided by time, or

Remembering that $f=1/T$, physicists (who like avoiding fractions when we can help it) will often write this as

This is called the wave equation.

As we mentioned in Wave Pulse, the speed of a wave depends on the medium the wave is travelling in, not on the wave itself. Thus if you have two waves moving through the same medium, then both will be travelling at the same speed $v$. If $v$ is constant, then the wave with the larger wavelength $\lambda$ must have the smaller frequency $f$, and vice versa.

Example

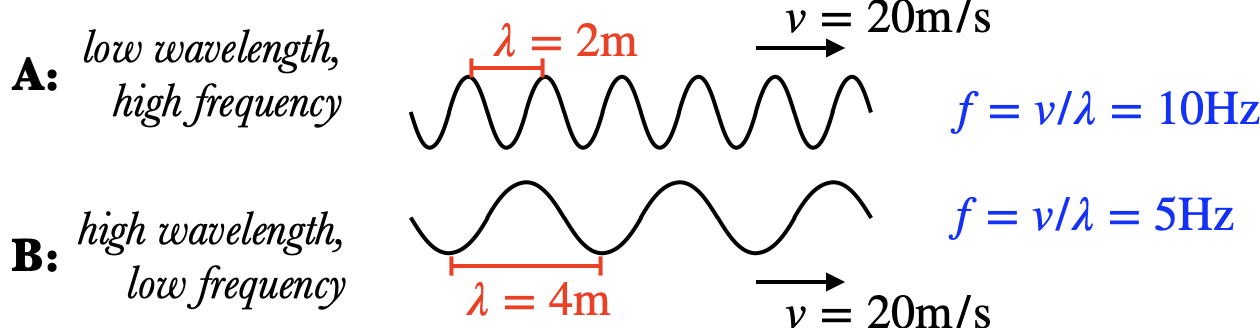
Two waves are moving through the same medium with a speed of $20\mathrm{m}/\mathrm{s}$. The first wave has a smaller wavelength of ${\lambda }_A=2\mathrm{m}$, and since $f=\frac{v}{\lambda }$, it has a frequency of $f_A=20/2=10\mathrm{Hz}$. The second wave has a larger wavelength of ${\lambda }_B=4\mathrm{m}$, so it has a smaller frequency of $f_B=20/4=5\mathrm{Hz}$.