Standing Waves
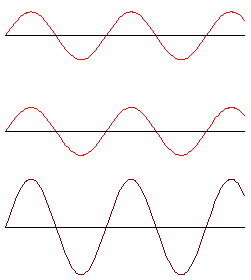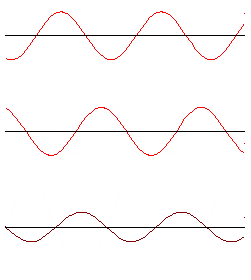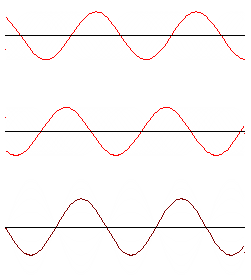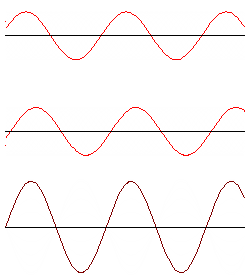
When a pulse reaches the edge of its medium, it will be reflected backwards. If it's a series of pulses, then the reflected pulses may interfere with the pulses that are following it. Most of the time the result is just a bit of a mess. However, if the frequency of the wave is just right, then the reflected pulse will be just in time to interfere constructively with the next subsequent pulse, and one gets a standing wave: unlike a normal wave, it doesn't move to the left or right.
For a string which is tied at both ends, or any other medium which cannot move at its endpoints, the standing waves will look like the ones on the right. The points that are not moving are called nodes, and the points that are moving the most are called antinodes. The number of antinodes in a standing wave is called its mode, and represented with the number $n$. There is a standing wave for every value of $n=1,2,3,\dots$.
Since each antinode here is half a wavelength apart, the total length $L$ of the wave is equal to $n\left(\frac12\lambda\right)$. If we rearrange this, we see that
The frequency of the wave is given by the wave equation: $f_n={v\over \lambda_n}$, so
where $f_1={v\over 2L}$ is called the fundamental frequency of the standing wave: the frequency of the $n=1$ mode. The frequency of the second mode is twice as fast, and so forth.