\(\def \u#1{\,\mathrm{#1}}\) \(\def \abs#1{\left|#1\right|}\) \(\def \ast{*}\) \(\def \deg{^{\circ}}\) \(\def \tau{\uptau}\) \(\def \ten#1{\times 10^{#1}}\) \(\def \redcancel#1{{\color{red}\cancel{#1}}}\) \(\def \BLUE#1{{\color{blue} #1}}\) \(\def \RED#1{{\color{red} #1}}\) \(\def \PURPLE#1{{\color{purple} #1}}\) \(\def \th#1,#2{#1,\!#2}\) \(\def \lshift#1#2{\underset{\Leftarrow\atop{#2}}#1}}\) \(\def \rshift#1#2{\underset{\Rightarrow\atop{#2}}#1}}\) \(\def \dotspot{{\color{lightgray}{\circ}}}\) \(\def \ccw{\circlearrowleft}\) \(\def \cw{\circlearrowright}\)
Chapter 10: Waves
11.

Doppler Effect

Think about what you hear when a loud car drives past you; you've probably even imitated in the sound in the past, as something like "yeeeeeee-OWWWWWWW". If you've heard an ice cream truck drive by playing music, you might have noticed that the song drops in pitch as the ice cream truck passes you. This is due to the Doppler effect. The Doppler effect occurs with all waves (in light it is often referred to as "redshift", and allows us to measure how fast stars are moving away from us), but we most frequently talk about it in the context of sound.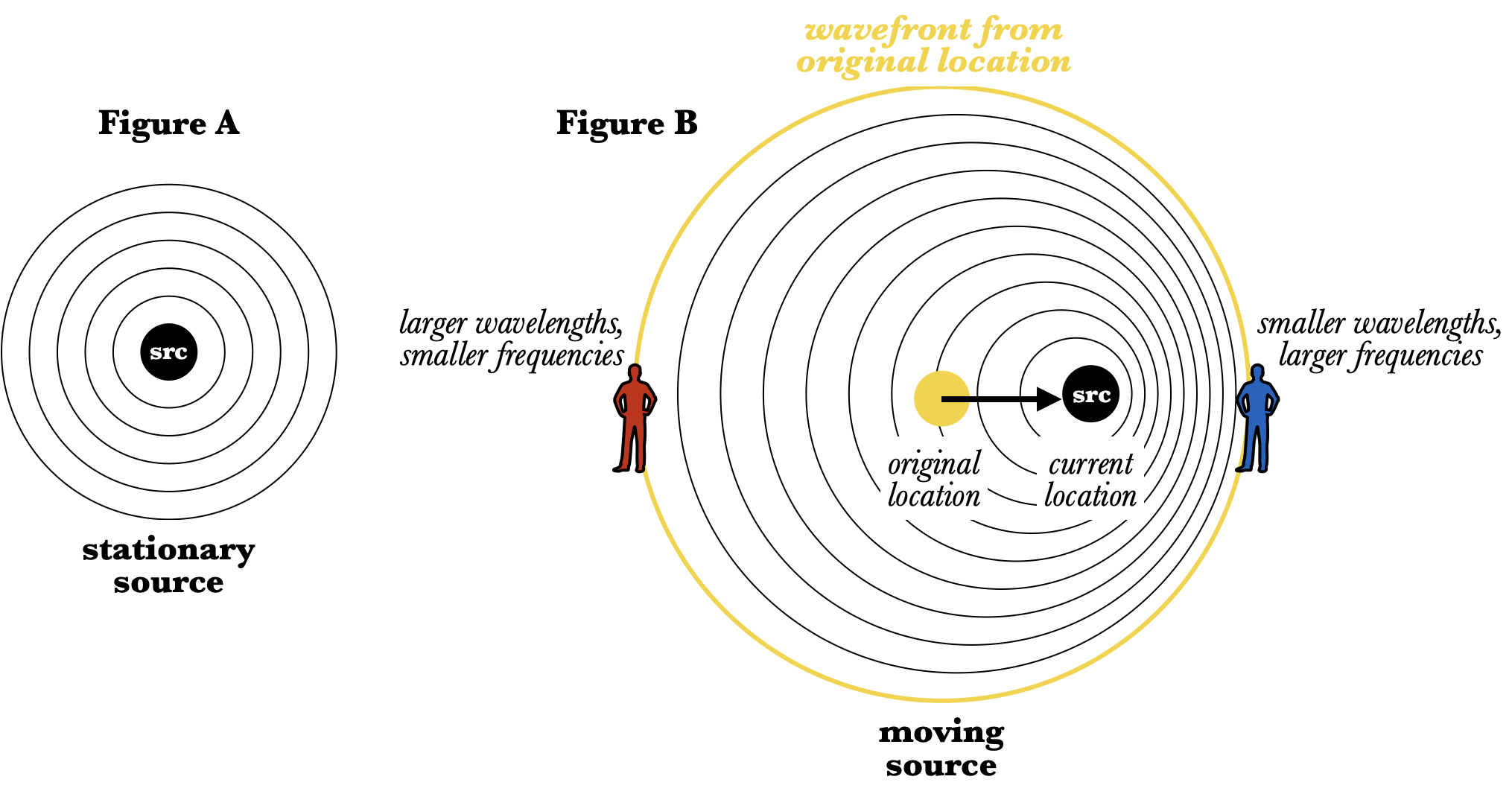

The left picture shows the wavefronts a stationary source of a sound. The wavefronts are spaced evenly in all directions, because the wavelength (and the frequency) are the same everywhere. In the right picture, on the other hand, the source is moving to the right. That means that each wavefront is centered on a spot a little bit to the right of the one that came after it. The result is that the wavefronts are closer together for the observer the source is moving towards, and smaller wavelengths mean higher frequencies (since $v=\lambda f$). The observer from whom the source is moving away, on the other hand, sees larger wavelengths and therefore hears smaller frequencies. You can play around with this effect in this demo:

We get a similar effect if the source is stationary and the observer is moving, though for a different reason. When an observer is running towards the source, they reach each wavefront a little sooner than they would have otherwise, and so they hear a higher frequency. When an observer is running away from the source, it takes a little longer for each wavefront to catch up to them, and so they hear a lower frequency.

Both these effects can be summed up as

If source and observer are moving towards each other, the frequency will increase.
If source and observer are moving away from each other, the frequency will decrease.

We can find the observed frequency numerically with the following formula:

$$f_{obs} = f_{src}{v_w\mp v_{obs}\over v_w\pm v_{src}}$$

where