Young's Two-Slit Interference

Young's two-slit experiment works in much the same way as in Interference: we set up two sources producing a single wavelength of light which are in phase with each other, and an interference pattern is formed.

In the modern version of the experiment, we shine laser light (guaranteed to be a single wavelength and in phase) through two parallel slits that are cut into opaque film. The two beams of light reunite on a screen a distance away, and depending on the different path lengths the two beams travelled, constructive or destructive interference may occur. The resulting pattern looks something like this:

The bright dots or fringes are places where constructive interference occurs between the two beams; the dark spaces in between are caused by destructive interference. The fringes are evenly spaced, each a distance $\Delta y$ from its neighbors.

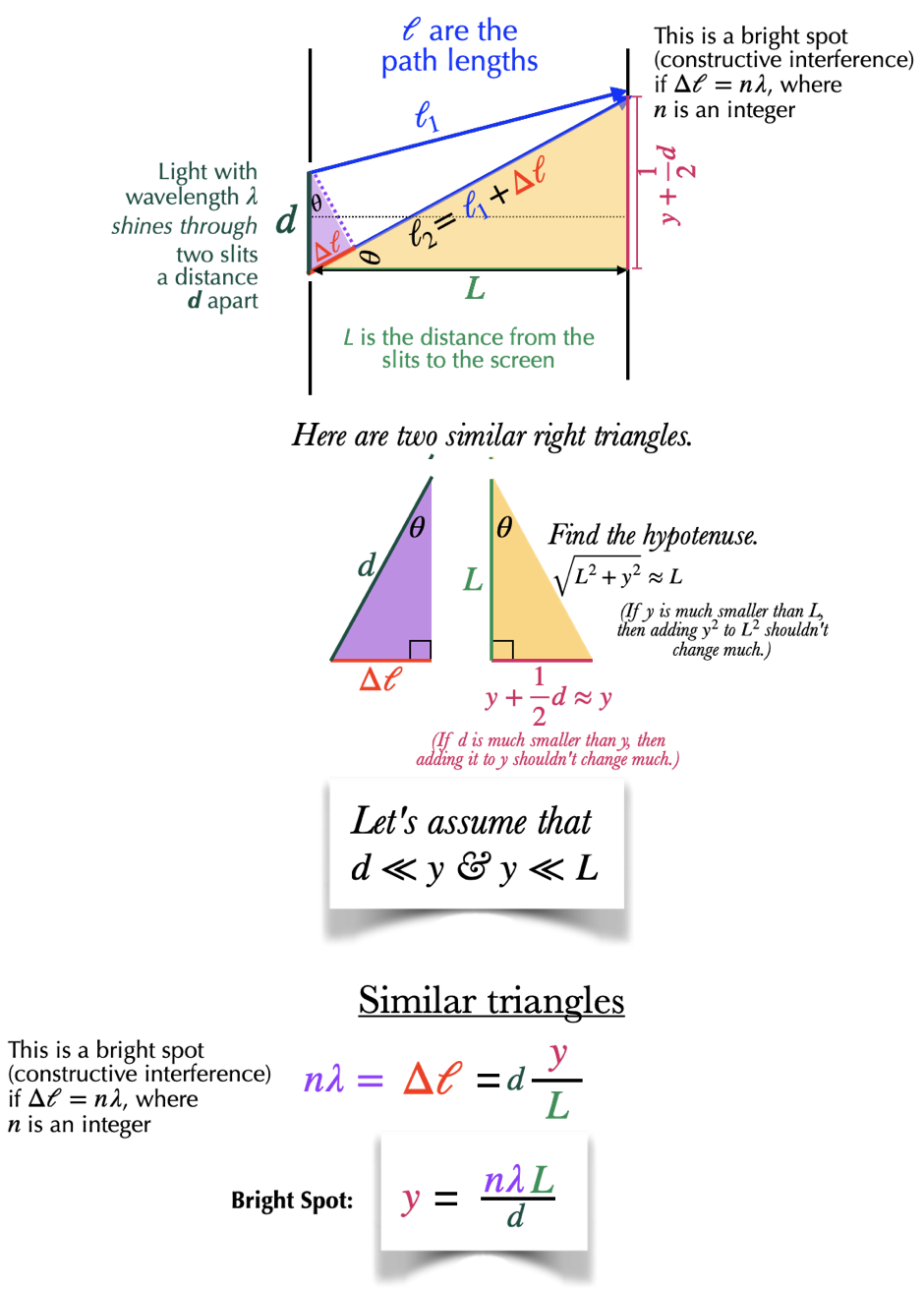
If we think of the central bright spot as the origin, then the position of the $n$th bright fringe is given by the formula

which is derived over on the right. The spacing between any two neighboring fringes is given by

The variables in these formulae are as follows:

• $n$ is called the order of the bright spot, as is pictured in the image above.
• $\lambda$ is the wavelength of the wave. For visible light, this is usually measured in nanometers. For example, $\lambda=500\u{nm}$ is green light. Larger wavelengths result in larger $y$, which means a wider pattern: the dots are wider and farther apart.
• $L$ is the distance from the slits to the screen: pull the screen farther away, and the pattern gets larger. This is exactly what happens for any projected image, so not really a surprise.
• $d$ is the distance between the two slits, usually measured in millimeters ($10^{-3}\u{m}$) or microns ($1\u{\mu m}=10^{-6}\u{m}$). Interestingly, the closer the two slits are to each other, the wider the pattern becomes.