Resolution
Diffraction plays an important role in how well an optical device (a telescope, microscope, or even our eyes) are able to distinguish details in an object. For example, the stars we see in the sky are basically point sources of light; they are much too small (at their distance) for us to notice any width. However, when the light from a star enters the pupil of our eyes, it creates a diffraction pattern on our retina. The central maximum of that pattern has a width of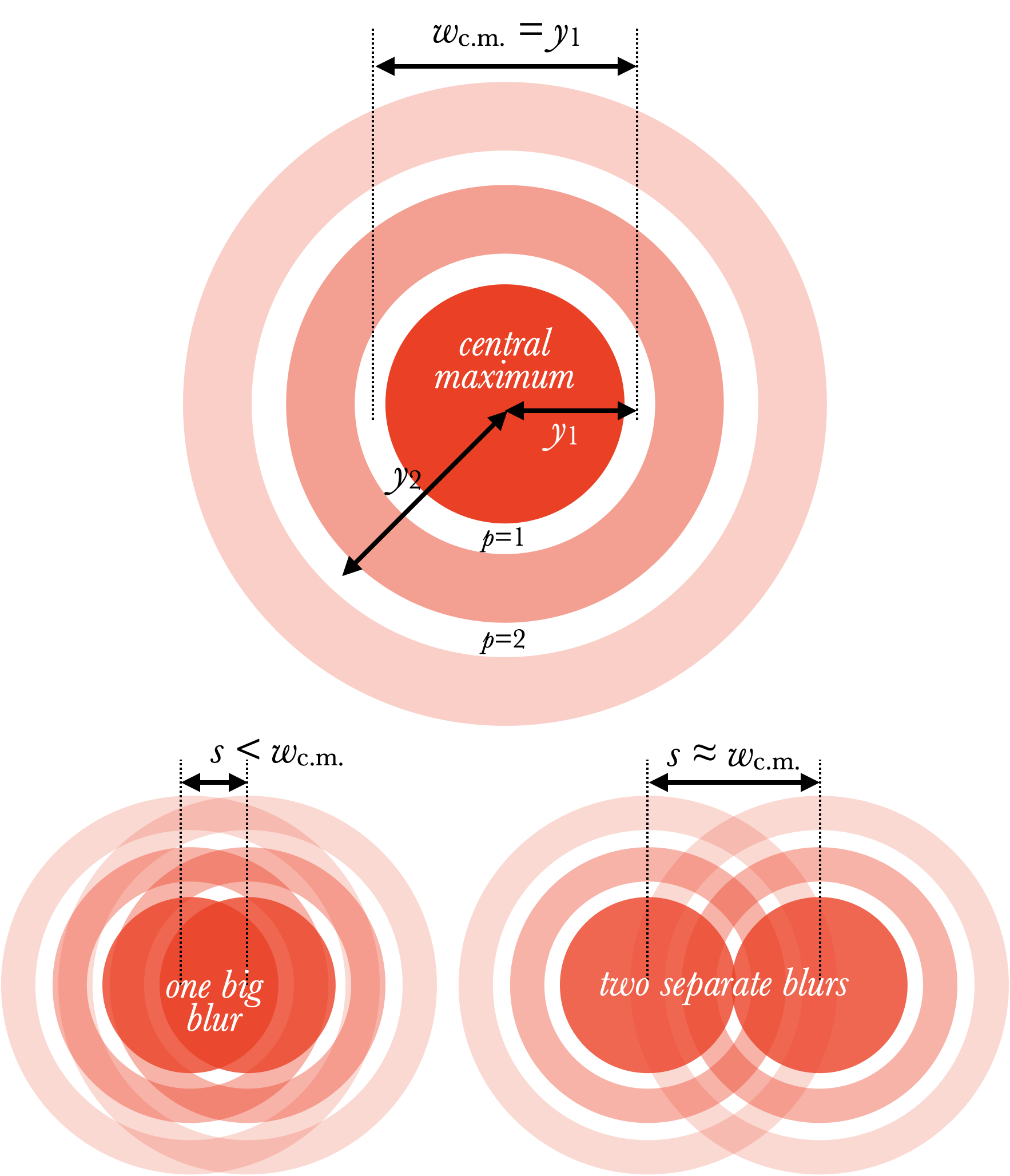
$$w_{c.m.}=2y_1 = 2.44{\lambda L\over a}$$ where $\lambda$ is the wavelength of the light, $a$ is the width of the aperture (like our pupils), and $L$ is the distance from the object to the eye. Instead of seeing a point, we see a smeared out blur of this size no matter how small the star is in the sky.
This blurring can make it difficult to distinguish between two different stars that are very close together. If the separation $s$ of the stars is less than the width of the central maximum, then the two blurs combine into a single blur; only when the stars are at least about $w_{c.m.}$ apart that they appear to be two separate light sources; in other words, the minimum separation between the two stars for them to be distinguishable is
When stargazing, it often makes more sense to talk about angular distances then the actual distance between the stars in space. The minimum angular separation for two sources to be distinguishable is
This is true for more than just stars, of course; it works for anything we see. Car headlights, for instance, will appear to be a single headlight when far enough away. And this phenomenon is not necessarily a bad thing for us! Televisions and computer screens only look good to us because our eyes are unable to see the individual pixels, but blur them together into a continuous image.