\(\def \u#1{\,\mathrm{#1}}\) \(\def \abs#1{\left|#1\right|}\) \(\def \ast{*}\) \(\def \deg{^{\circ}}\) \(\def \redcancel#1{{\color{red}\cancel{#1}}}\) \(\def \BLUE#1{{\color{blue} #1}}\) \(\def \RED#1{{\color{red} #1}}\) \(\def \PURPLE#1{{\color{purple} #1}}\) \(\def \th#1,#2{#1,\!#2}\) \(\def \lshift#1#2{\underset{\Leftarrow\atop{#2}}#1}}\) \(\def \rshift#1#2{\underset{\Rightarrow\atop{#2}}#1}}\) \(\def \dotspot{{\color{lightgray}{\circ}}}\)

Initial Phase

The initial phase $\phi_0$ of an oscillation can be read from its history graph depending on what its displacement $y(t)$ is doing at $t=0$: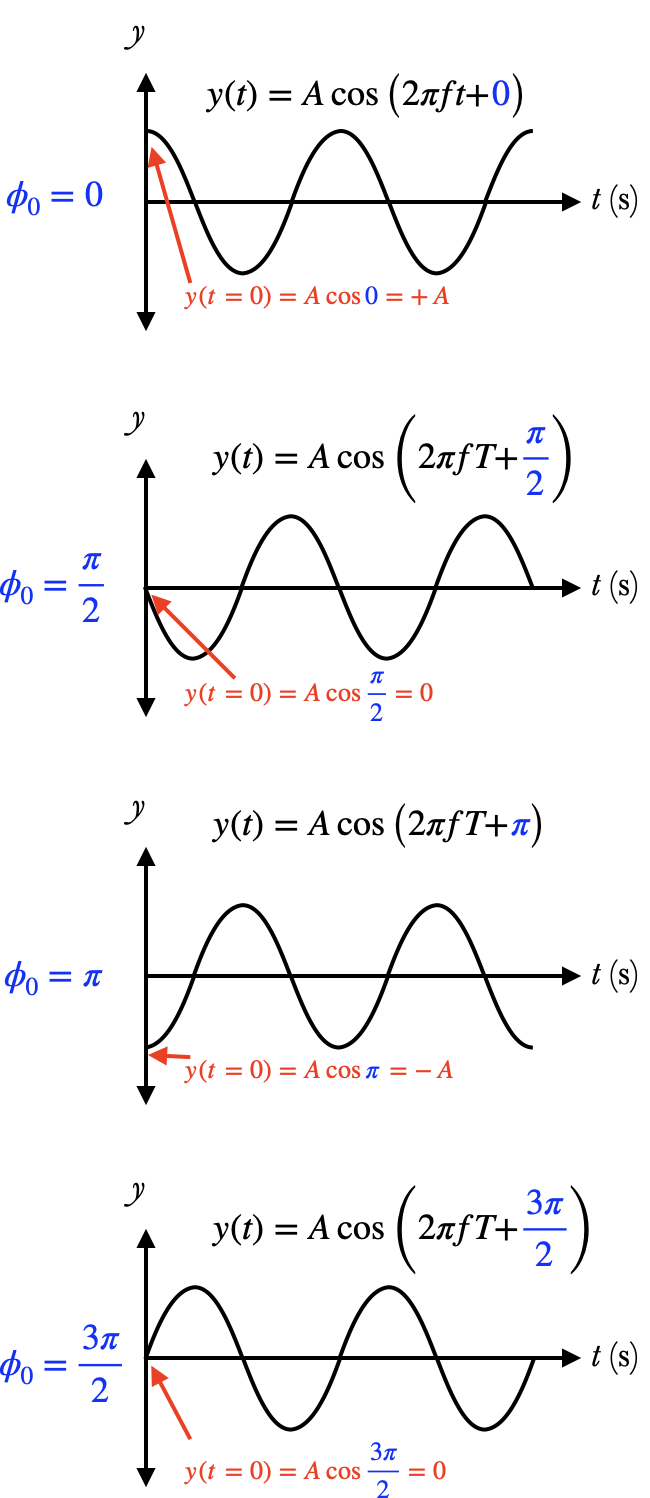

• If the displacement is at its maximum at $t=0$, then $\phi_0=0$
• If the displacement is at equilibrium and moving in the negative direction, then $\phi_0={\pi\over 2}\approx 1.57$
• If the displacement is at its minimum, then $\phi_0=\pi\approx 3.14$
• If the displacement is at equilibrium and moving in the positive direction, then $\phi_0={3\pi\over2}\approx 4.71$