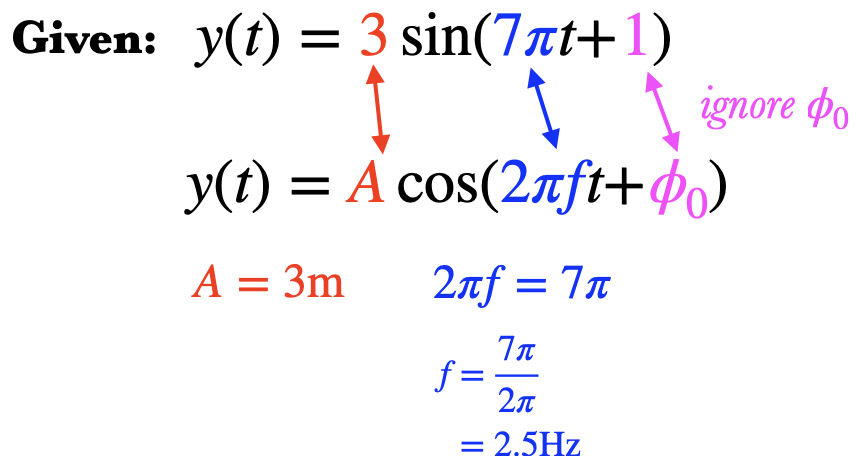\(\def \u#1{\,\mathrm{#1}}\) \(\def \abs#1{\left|#1\right|}\) \(\def \ast{*}\) \(\def \deg{^{\circ}}\) \(\def \redcancel#1{{\color{red}\cancel{#1}}}\) \(\def \BLUE#1{{\color{blue} #1}}\) \(\def \RED#1{{\color{red} #1}}\) \(\def \PURPLE#1{{\color{purple} #1}}\) \(\def \th#1,#2{#1,\!#2}\) \(\def \lshift#1#2{\underset{\Leftarrow\atop{#2}}#1}}\) \(\def \rshift#1#2{\underset{\Rightarrow\atop{#2}}#1}}\) \(\def \dotspot{{\color{lightgray}{\circ}}}\)

Using Formulas

If you know the amplitude, frequency (or period), and the Initial Phase of an oscillation, you can find its displacement, velocity, or acceleration at any time $t$ by using these formulas: $$y(t)=A\cos(2\pi ft+\phi_0)$$ $$v(t)=-2\pi fA\sin(2\pi ft+\phi_0)$$ $$a(t)=-4\pi^2f^2A\cos(2\pi ft+\phi_0)$$

If you're given a formula for one of these things (but with numbers instead of letters), and you want to figure out the amplitude, frequency, and initial phase, write the original formula above the given formulae and match corresponding pieces. For instance

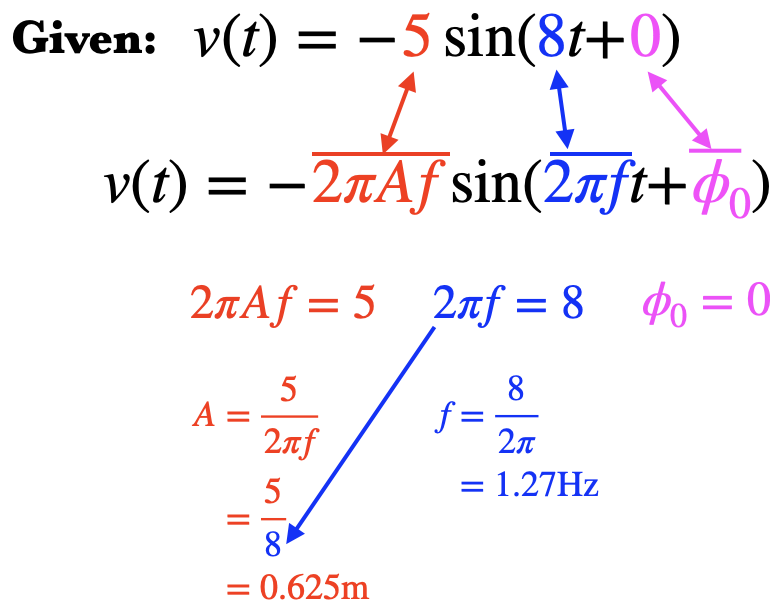
Note that if you're given a formula but it's a cosine instead of a sine (or vice versa), or if the sign out front is wrong, you can still get the frequency and amplitude in the same way; the initial phase, however, will be incorrect: