What Are Oscillations?

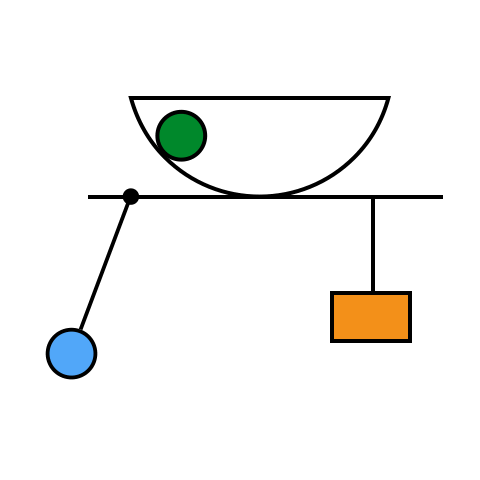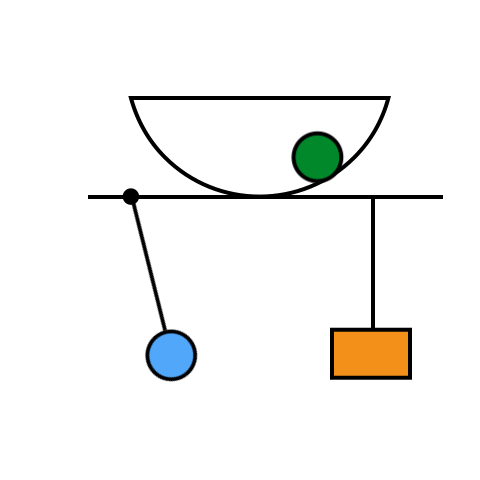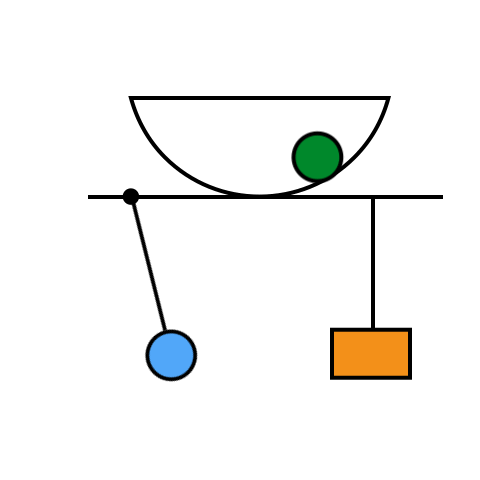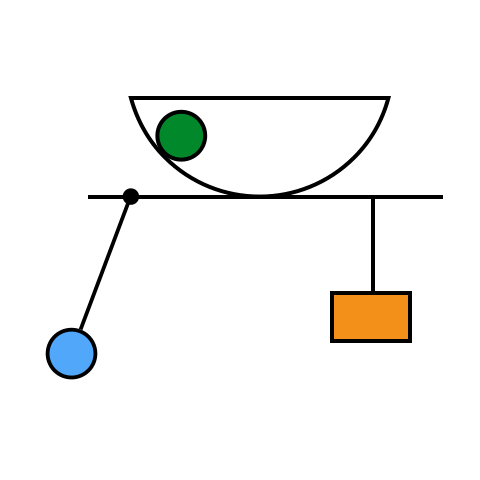
An oscillation is a periodic back-and-forth motion in a physical system. A pendulum swinging back and forth, a block bouncing on a spring, a ball rolling back and forth in a bowl—all of these are oscillations. A cycle of an oscillation is one repetition of the back-and-forth motion: at the end of the cycle, the system will be in the same place, and moving at the same velocity, as it was at the beginning of the cycle. The time it takes for a cycle to complete is called the oscillation period, which we'll discuss more later .

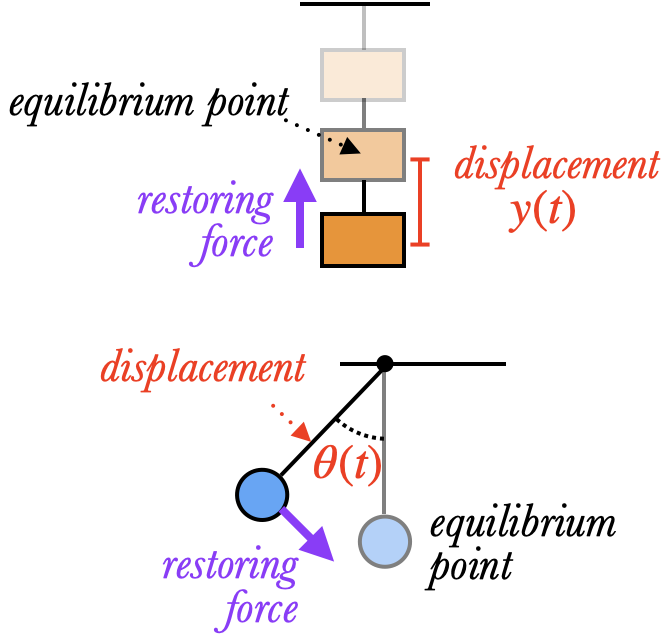
In every oscillation there is a certain middle point that the system oscillates around, called the equilibrium point. If the object is placed at the equilibrium point and let go, it won't oscillate at all, but will just sit there. If the object is moved slightly away from the equilibrium point, it will feel a restoring force that pushes it back to the equilibrium point. Because of Newton's Second Law, the object accelerates as it heads back to the equilibrium point, so that when it reaches the equilibrium point it has some velocity. It can't immediately stop at the equilibrium point, however, because of the law of inertia: instead, the object keeps moving to the other side of the equilibrium point, where it is pulled back again to the equilibrium point, and so the oscillation repeats itself over and over.

The distance of the object from its equilibrium point is called its displacement, and is a function of time. Displacement can be measured in different units, depending on the system. For the block on a spring, the displacement is a distance, and is measured in meters (and usually written $y(t)$). For a pendulum, the displacement is an angle $\theta(t)$, and record it in radians. One can find more abstract forms of oscillation in physics as well: for instance, in alternating current the voltage oscillates around zero, and so the displacement of the current is measured in volts $V(t)$.

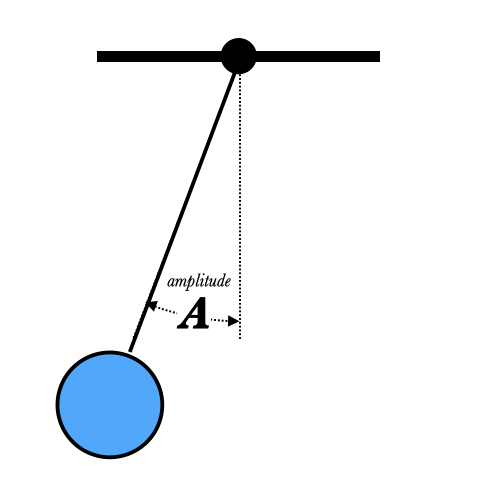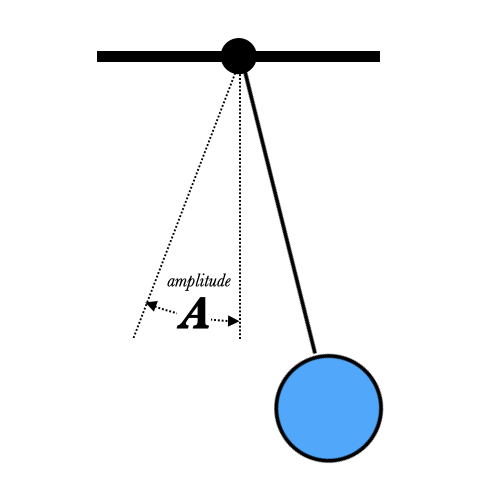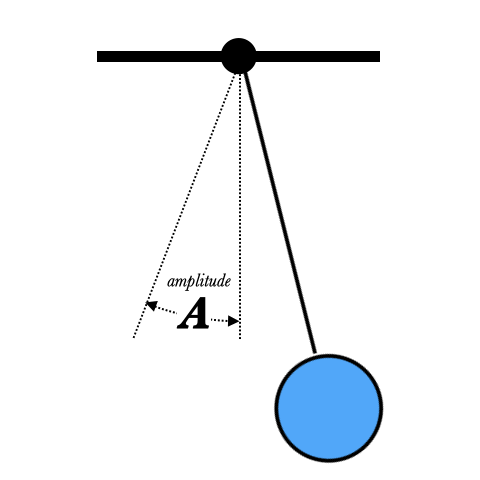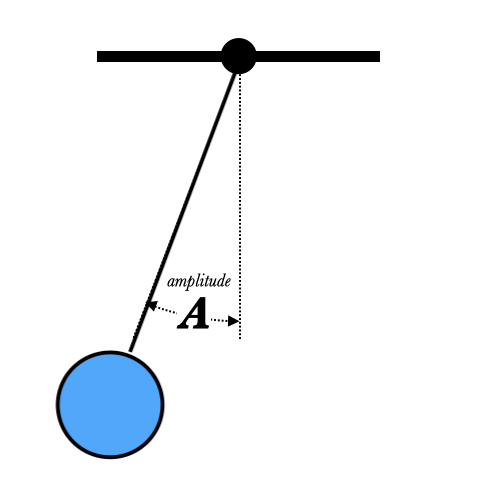
The amplitude $A$ of an oscillation is the maximum (positive) displacement of the object, and has the same units as the displacement.