Velocity and Acceleration
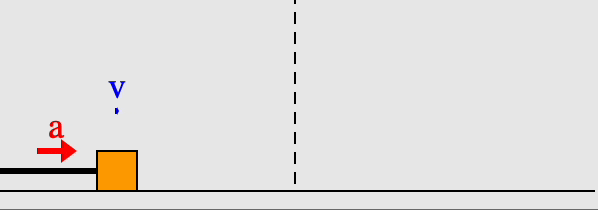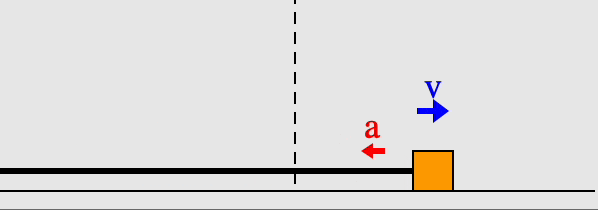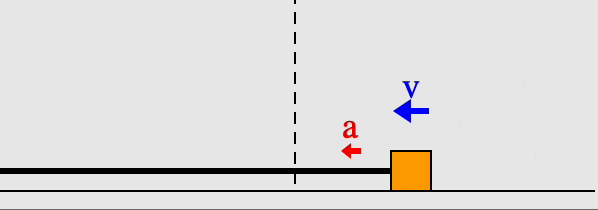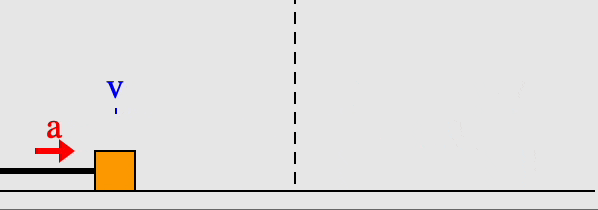
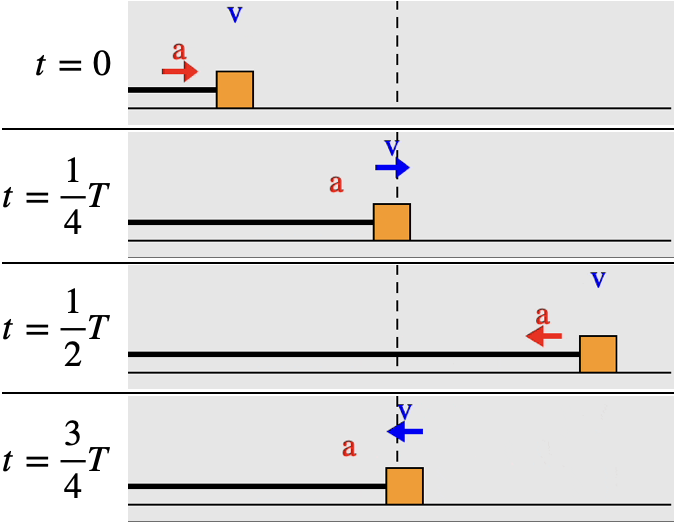
A block on a spring is an example of simple harmonic motion. In the animation here, we see the block oscillating around either side of the equilibrium point, marked with the dashed line. The extreme ends of the block's motion are turning points, where the velocity is zero. The acceleration is zero at the equilibrium point in the center, on the other hand, because there the net force on the block is zero, and $a=F_{net}/m$.
If we graph the displacement, velocity, and acceleration of simple harmonic motion, we see that they are all sinusoidal with the same period:
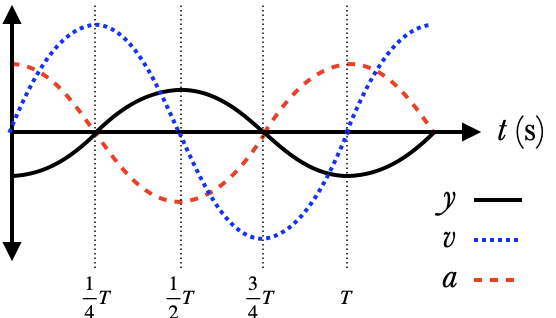
While they have the same period, they are shifted horizontally, and they have different vertical sizes. The formulas for the three curves are $$y(t) = A\cos (2\pi ft + \phi_0)$$ $$v(t) = -v_{\max}\sin (2\pi ft + \phi_0)$$ $$a(t) = -a_{\max}\cos (2\pi ft + \phi_0)$$ where
(If you know calculus, you'll notice that $v$ is the derivative of $y$ and $a$ is the derivative of $a$, as they should be.)