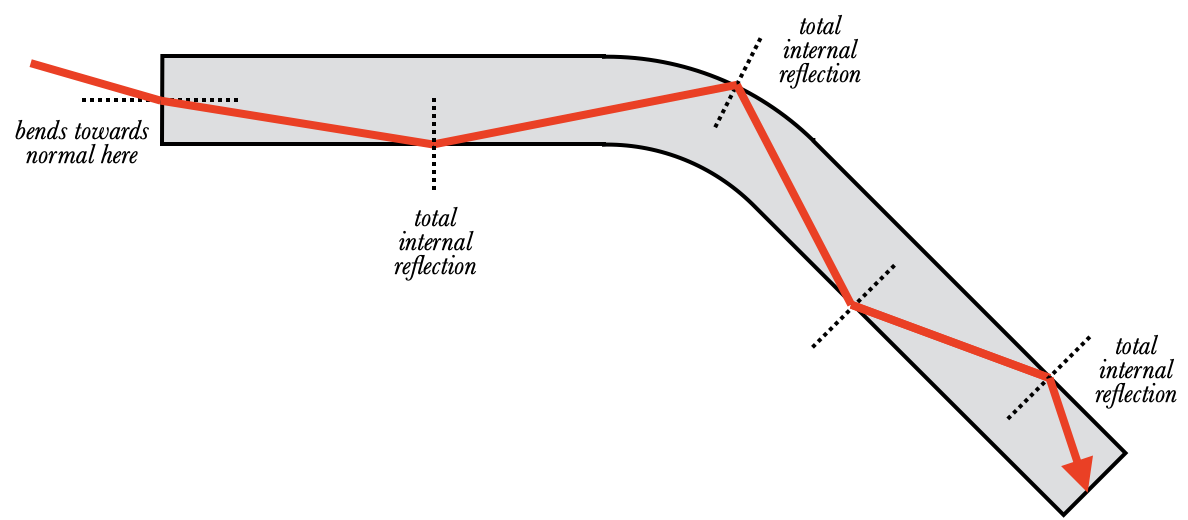
Total Internal Reflection

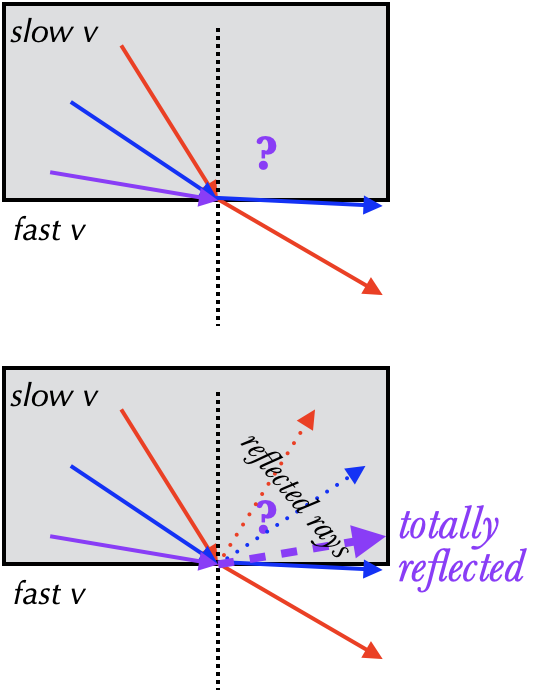
When light moves from a "slower material" (i.e. a material where the speed of light is faster) to a faster material, it bends away from the normal. This can cause a problem if it needs to bend TOO far from the normal. What happens then?

You might guess that the ray goes back into the original material, and you'd be right...in a way. Remember that whenever light moves from one material to another, there's always a possibility of reflection, and so a more accurate picture of the image above would include the reflected rays as well as the transmitted rays. When a ray is unable to bend far enough in the fast material, it just doesn't come out at all; instead all of the ray is reflected. This only occurs when light tries to speed up, and since the most common case of this is when light tries to escape from water or glass or whatever into air, we call it total internal reflection.

EXAMPLE: If $n_i=1$, $n_t=1.3$, and $\sin\theta_i=0.9$, then $$\sin\theta_t = {1\over 1.3}(0.9) = 0.69$$ which is fine.

But if $n_i=1.3$ and $n_t=1$, then $$\sin\theta_t = {1.3\over 1}(0.9) = 1.17$$ and there's no solution for that.

To see why this occurs, let's rearrange Snell's Law a bit: $$\sin\theta_t = {n_i\over n_t}\sin\theta_i$$ Recall that the sine function can never be greater than 1. If $n_in_t$, then the fraction $n_i\over n_t$ is larger than 1, and if $\sin\theta_i$ is also large, it's possible that $\sin\theta_t$ will need to be greater than 1. That's not possible, and so total internal reflection occurs when there is no solution to Snell's Law.

In other words, total internal reflection occurs when $$\begin{align} {n_i\over n_t}\sin\theta_i &> 1\\ \implies \sin\theta_i &>{n_t\over n_i}\\ \implies \theta_i &>\sin^{-1}{n_t\over n_i}\\ \end{align}$$

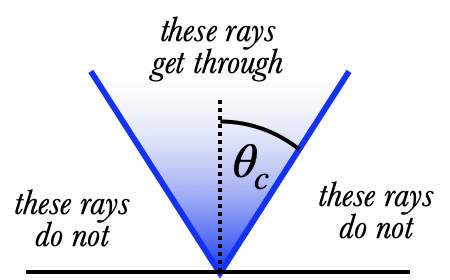
The smallest incident angle at which this inequality holds, is called the critical angle:

$$\theta_c = \sin^{-1}{n_t\over n_i}$$

where $n_i$ is the index of the material the light is trying to leave, and $n_t$ is the index of the material it's trying to get into. Rays which hit the interface at an angle smaller than $\theta_c$ will at least partially pass through; rays with a larger angle will not.

Uses

The index of refraction of diamond is $n=2.4$, so its critical angle is $\sin^{-1}{1\over 2.4}=24.6\deg$. That means when a ray inside diamond hits an interface at a random angle, it only has a ${24.6\deg\over 90\deg}=27\%$ chance of escaping. When light enters a cut diamond from a local light source, therefore, the light spends a lot of time bouncing around inside before it is able to escape in a random direction. Shift the diamond slightly, and the angles may change enough for the ray to emerge in a completely different location. This is why diamonds are "sparkly", in fact more sparkly than glass, which has a critical angle of about $42\deg$.

A more practical use of total internal reflection is in the construction of fiber optics cables, which are used for fast information transmission, endoscopy, and other things. A fiber optic cable is just a simple thin "thread" of glass or other transparent material, very pure with no cracks or bubbles inside. When a ray of light enters one end, it bounces off alternating sides of the glass, but so long as the glass doesn't bend too much, the angles of incidence are always so large that total internal reflection occurs. The (ideal) result: the ray of light travels from one end of the fiber optic cable to the other without any light (and thus any signal) being lost. In practice, light can scatter off of small imperfections in the glass and so hit the surface at a smaller angle, letting some of the light escape.

(no alternate text) — A fiber-optic cable.