\(\def \u#1{\,\mathrm{#1}}\) \(\def \abs#1{\left|#1\right|}\) \(\def \ast{*}\) \(\def \deg{^{\circ}}\) \(\def \ten#1{\times 10^{#1}}\) \(\def \redcancel#1{{\color{red}\cancel{#1}}}\) \(\def \BLUE#1{{\color{blue} #1}}\) \(\def \RED#1{{\color{red} #1}}\) \(\def \PURPLE#1{{\color{purple} #1}}\) \(\def \th#1,#2{#1,\!#2}\) \(\def \lshift#1#2{\underset{\Leftarrow\atop{#2}}#1}}\) \(\def \rshift#1#2{\underset{\Rightarrow\atop{#2}}#1}}\) \(\def \dotspot{{\color{lightgray}{\circ}}}\)

Magnification

An image is often a different size than the original object. The amount by which the size changes is called the image's magnification:

where the variables $h_o$ and $h_i$ are the height of the object and the height of the image, respectively. (We say "height", but really we could use the width, or the length of any corresponding parts of object and image: they all scale in the same way.) If the object is inverted, then the magnification is negative. You can think of the magnification as a percentage if you like: $M=0.75$ means the image is 75% the size of the object, while $M=-3$ means the image is inverted and 300% times the size of the object.

If you've ever played with a projector of any sort, you probably know that as you move the projector (and thus the lens) away from the screen (the image), the image gets larger. In fact, magnification can also be written as

where $d_o$ and $d_i$ are the distances of the object and the image from the lens, respectively, as we discussed before. Remember from before that $d_o$ is positive, while a positive $d_i$ means the image is real? Well if both are positive, then the magnification is negative, which means that real images are inverted. For virtual images, on the other hand, $-{d_i\over d_o}$ is positive, and the image is upright.

Using the solved version of the lens equation $d_i={d_of\over d_o-f}$ from before, we can write the magnification as $$M=-{d_i\over d_o} = -{f\over d_o-f}$$ If we graph this, we see that a converging lens or mirror has three different regimes:

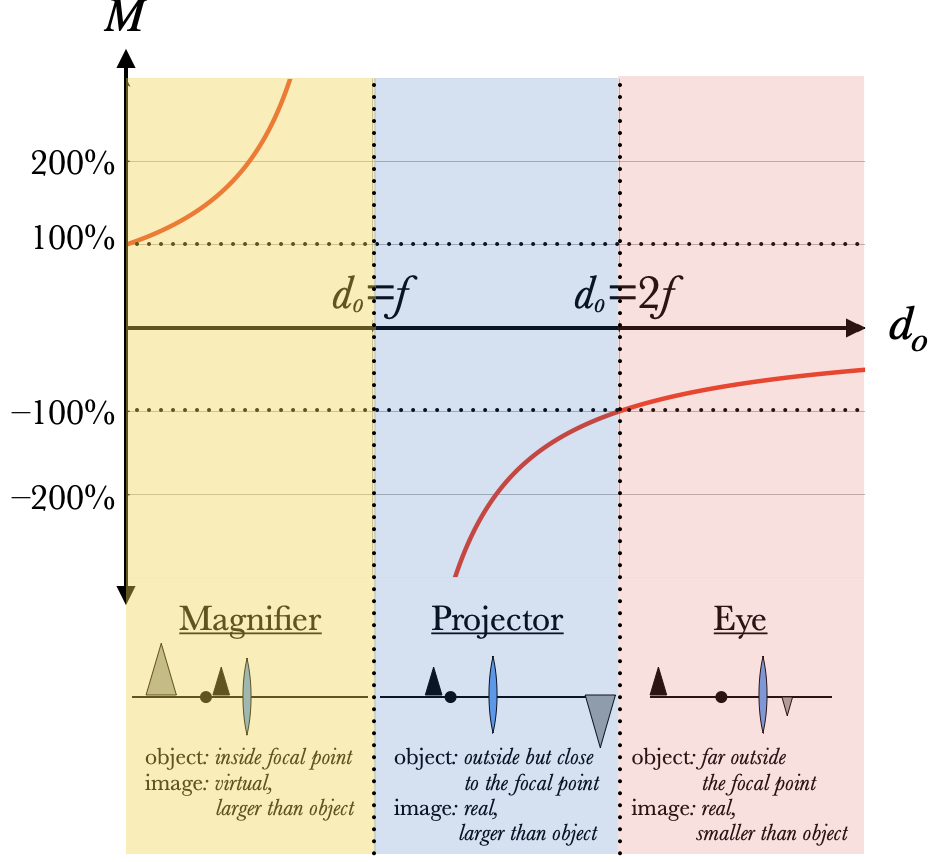
1. If $f<d_o-f$ (or $d_o>2f$), then the magnification $|M|$ is smaller than 1, and the image is real, inverted and small. An example of this is the eye (or a camera), where the object is usually much larger and much farther from the lens than the retina on which the image is projected.
2. If $d_o<2f$ but $d_o>f$ (so the denominator is still positive), then the magnification $|M|$ is larger than 1 (or 100%), and the image is larger than the object. A projector falls into this regime: the object itself is a tiny transluscent LCD monitor close to the lens (and upside-down), and we see the much bigger image on the screen.
3. If $d_o<f$, then the denominator is negative, and the magnification is positive: we have a virtual image, which cannot be projected, and one which is larger than the object. An example of this is a magnifying glass, which creates larger images of the same object, right-side up, and the image appears on the same side of the lens as the object.