\(\def \u#1{\,\mathrm{#1}}\) \(\def \abs#1{\left|#1\right|}\) \(\def \ast{*}\) \(\def \deg{^{\circ}}\) \(\def \tau{\uptau}\) \(\def \ten#1{\times 10^{#1}}\) \(\def \redcancel#1{{\color{red}\cancel{#1}}}\) \(\def \BLUE#1{{\color{blue} #1}}\) \(\def \RED#1{{\color{red} #1}}\) \(\def \PURPLE#1{{\color{purple} #1}}\) \(\def \th#1,#2{#1,\!#2}\) \(\def \lshift#1#2{\underset{\Leftarrow\atop{#2}}#1}}\) \(\def \rshift#1#2{\underset{\Rightarrow\atop{#2}}#1}}\) \(\def \dotspot{{\color{lightgray}{\circ}}}\) \(\def \ccw{\circlearrowleft}\) \(\def \cw{\circlearrowright}\)
Chapter 3: Linear Motion
2.

Displacement Vectors

Note

Note that "$\Delta x$" does not mean $\Delta\times x$ here. $\Delta$ means "change" or "difference", and $\Delta x$ is the change in the object's position from one moment to the next.

The arrows between the dots are called displacement vectors, and are usually represented by the symbol $\Delta x$.

Displacement
\(\Delta x\)
meters (m)
The magnitude (or length) of the displacement vector is the distance the car travelled between one dot and the next, and is measured in meters.

Here are some more examples of motion diagrams.

Column

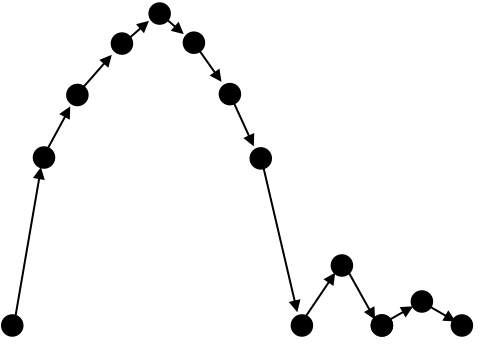
(no alternate text)

ball thrown in the air hits the ground and bounces

Column

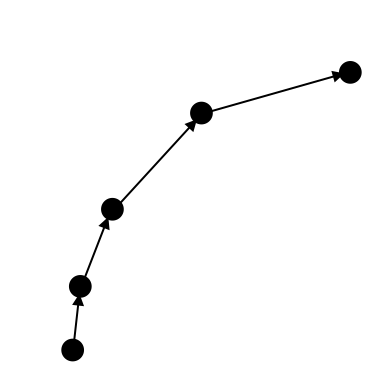
(no alternate text)

car speeding up as it goes around a corner

Column

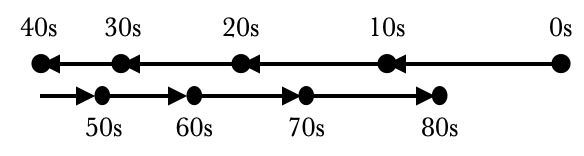
(no alternate text)

A car comes to a stop and then goes in reverse. The late dots are shifted downward to avoid overlap and confusion.