Constant Acceleration
When the acceleration of an object is constant, there are a set of equations we can use to predict how that object will move. Consider the motion of the object between some initial moment i and some final moment f. There are five variables we need to completely describe its motion:
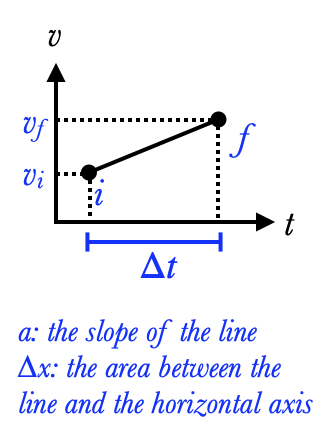
- the time Δt it takes to travel from i to f
- its initial velocity vi
- its final velocity vf
- its acceleration a
- the displacement Δx between its initial position and its final position
We already know two equations we can use to solve for these five variables. The first is the definition of acceleration (right), which can be rewritten without fractions as
The second is the definition of average velocity $\bar v={\Delta x\over \Delta t}$, with the fact (here unproved) that when the acceleration is constant, the average velocity is the average of $v_i$ and $v_f$, giving us
Two equations allow us to solve for two unknowns, which means that we need to be given three of the five variables above to solve for the rest. That's worth repeating:
we must be given three of the five variables
in order to solve for the rest.